+ - 0:00:00
Notes for current slide
Notes for next slide

3.1 — The Problem of Causal Inference

ECON 480 • Econometrics • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF21
metricsF21.classes.ryansafner.com

Outline

First Pass at Causation: RCTs

Potential Outcomes

Natural Experiments

Attack of/on the Randomistas

Different Uses for Statistics & Econometrics

Y=f(X)

  1. Causal inference: how changes in X cause changes in Y

    • Care more about accurately estimating f than getting an accurate ˆY
    • Measure the causal effect of X↦Y (e.g., ^β1)

  2. Prediction: predict ˆY using an estimated f

    • Care more about getting ˆY as accurate as possible, f is an unknown “black-box”
    • Forecasting: predict future values of Y (inflation, sales, GDP)
    • Classification: predict the category of an outcome (success or failure, cat picture or not cat picture)
  • We care (in this class at least) only about the first

Recall: The Two Big Problems with Data

  • We use econometrics to identify causal relationships and make inferences about them

  1. Problem for identification: endogeneity

    • X is exogenous if cor(x,u)=0
    • X is endogenous if cor(x,u)≠0

  2. Problem for inference: randomness

    • Data is random due to natural sampling variation
    • Taking one sample of a population will yield slightly different information than another sample of the same population

The Two Problems: Identification and Inference

Sample statistical inference→ Population causal indentification→ Unobserved Parameters

The Two Problems: Identification and Inference

Sample statistical inference→ Population causal indentification→ Unobserved Parameters

  • We saw how to statistically infer values of population parameters using our sample
    • Purely empirical, math & statistics 🤓

The Two Problems: Identification and Inference

Sample statistical inference→ Population causal indentification→ Unobserved Parameters

  • We saw how to statistically infer values of population parameters using our sample

    • Purely empirical, math & statistics 🤓

  • We now confront the problem of identifying causal relationships within population

    • Endogeneity problem
    • Even if we had perfect data on the whole population, “Does X truly cause Y?”, and can we measure that effect?
    • More philosophy & theory than math & statistics! 🧐

  • Truly you should do this first, before you get data to make inferences!

What Does Causation Mean?

  • We are going to reflect on one of the biggest problems in epistemology, the philosophy of knowledge

  • We see that X and Y are associated (or quantitatively, correlated), but how do we know if X causes Y?

First Pass at Causation: RCTs

Random Control Trials (RCTs) I

  • The ideal way to demonstrate causation is through a randomized control trial (RCT) or "random experiment"

    • Randomly assign experimental units (e.g. people, firms, etc.) into groups
    • Treatment group(s) get a (kind of) treatment
    • Control group gets no treatment
    • Compare results of treatment and control groups to observe the average treatment effect (ATE)

  • We will understand “causality” (for now) to mean the ATE from an ideal RCT

Random Control Trials (RCTs) II

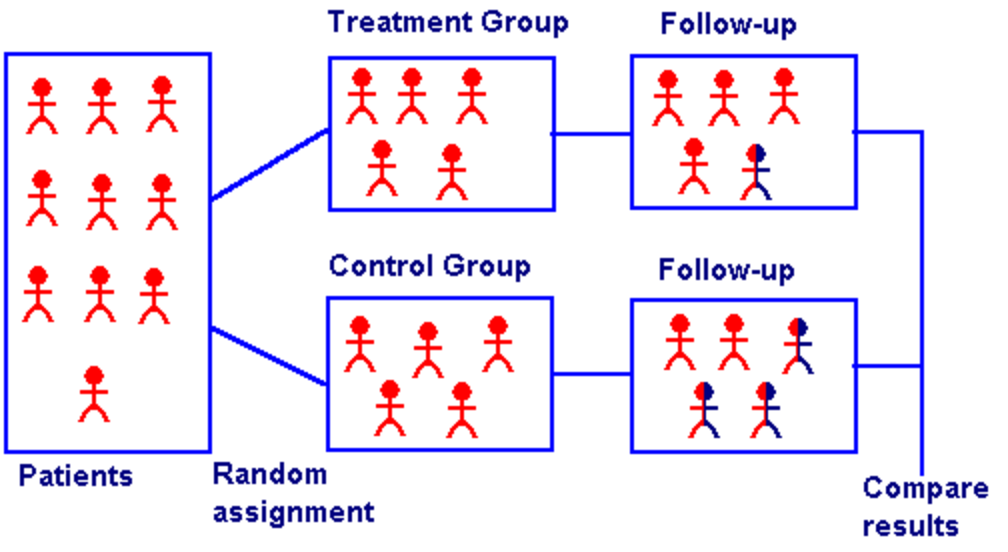
Classic (simplified) procedure of a randomized control trial (RCT) from medicine

Random Control Trials (RCTs) III

Random Control Trials (RCTs) IV

  • Random assignment to groups ensures that the only differences between members of the treatment(s) and control groups is receiving treatment or not

Treatment Group

Control Group

Random Control Trials (RCTs) IV

  • Random assignment to groups ensures that the only differences between members of the treatment(s) and control groups is receiving treatment or not

  • Selection bias: (pre-existing) differences between members of treatment and control groups other than treatment, that affect the outcome

Treatment Group

Control Group

(Selection Bias)

Potential Outcomes

The Fundamental Problem of Causal Inference

  • Suppose we have some outcome variable Y

The Fundamental Problem of Causal Inference

  • Suppose we have some outcome variable Y

  • Individuals (i) face a choice between two outcomes (such as being treated or not treated):

    • Y0i: outcome when individual i is not treated
    • Y1i: outcome when individual i is treated

The Fundamental Problem of Causal Inference

  • Suppose we have some outcome variable Y

  • Individuals (i) face a choice between two outcomes (such as being treated or not treated):

    • Y0i: outcome when individual i is not treated
    • Y1i: outcome when individual i is treated

✨ δi=Y1i−Y0i ✨

  • δi is the causal effect of treatment on individual i

The Fundamental Problem of Causal Inference

✨ δi=Y1i−Y0i ✨

The Fundamental Problem of Causal Inference

✨ δi=Y1i−Y0i ✨

  • This is a nice way to think about the ideal proof of causality, but this is impossible to observe!

The Fundamental Problem of Causal Inference

δi=?−Y0i

  • This is a nice way to think about the ideal proof of causality, but this is impossible to observe!

  • Individual counterfactuals do not exist (“the path not taken”)

  • You will always only ever get one of these per individual!

The Fundamental Problem of Causal Inference

δi=Y1i−?

  • This is a nice way to think about the ideal proof of causality, but this is impossible to observe!

  • Individual counterfactuals do not exist (“the path not taken”)

  • You will always only ever get one of these per individual!

    • e.g. what would your life have been like if you did not go to Hood College?? 🧐

  • So what can we do?

The Fundamental Problem of Causal Inference

ATE=E[Y1i]−E[Y0i]

  • Have large groups, and take averages instead!

  • Average Treatment Effect (ATE): difference in the average (expected value) of outcome Y between treated individuals and untreated individuals δ=(ˉY|D=1)−(ˉY|D=0)

  • Di is a binary variable, ={0 if person is not treated1 if person is treated

    • I’d much rather call this Ti, standing for Treatment, but this notation is famous

The Fundamental Problem of Causal Inference

ATE=E[Y1i]−E[Y0i]

Again:

  • Either we observe individual i in the treatment group (D=1), i.e. δi=Y1i−?

  • Or we observe individual i in the control group (D=0), i.e. δi=?−Y0i

  • Never both at the same time:

    ✨ δi=Y1i−Y0i ✨

Example: The Effect of Having Health Insurance I

Example: What is the effect of having health insurance on health outcomes?

  • National Health Interview Survey (NHIS) asks “Would you say your health in general is excellent, very good, good, fair, or poor?”

  • Outcome variable (Y): Index of health (1-poor to 5-excellent) in a sample of married NHIS respondents in 2009 who may or may not have health insurance

  • Treatment (X): Having health insurance (vs. not)

Example: The Effect of Having Health Insurance II

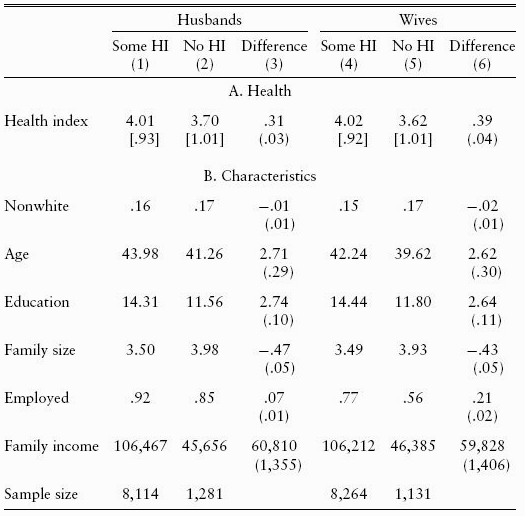
Angrist, Joshua & Jorn-Steffen Pischke, 2015, Mostly Harmless Econometrics

Example: The Effect of Having Health Insurance III

  • Y: outcome variable (health index score, 1-5)

  • Yi: health score of an individual i

  • Individual i has a choice, leading to one of two outcomes:

    • Y0i: individual i has not purchased health insurance (“Control”)
    • Y1i: individual i has purchased health insurance (“Treatment”)

  • δi=Y1i−Y0i: causal effect for individual i of purchasing health insurance

Example: A Hypothetical Comparison

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5

Example: A Hypothetical Comparison

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5

  • John will choose to buy health insurance

  • Maria will choose to not buy health insurance

Example: A Hypothetical Comparison

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5
✨ δJ=1 δM=0 ✨

  • John will choose to buy health insurance

  • Maria will choose to not buy health insurance

  • Health insurance improves John's score by 1, has no effect on Maria's score (individual causal effects δi)

Example: A Hypothetical Comparison

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5
✨ δJ=1 δM=0 ✨
YJ=(Y1J)=4 YM=(Y0M)=5

  • John will choose to buy health insurance

  • Maria will choose to not buy health insurance

  • Health insurance improves John's score by 1, has no effect on Maria's score (individual causal effects δi)

  • Note, all we can observe in the data are their health outcomes after they have chosen (not) to buy health insurance: YJ=4YM=5

Example: A Hypothetical Comparison

John Maria
Y0J=3 Y0M=5
Y1J=4 Y1M=5
✨ δJ=1 δM=0 ✨
YJ=(Y1J)=4 YM=(Y0M)=5

  • John will choose to buy health insurance

  • Maria will choose to not buy health insurance

  • Health insurance improves John's score by 1, has no effect on Maria's score (individual causal effects δi)

  • Note, all we can observe in the data are their health outcomes after they have chosen (not) to buy health insurance: YJ=4YM=5

  • Observed difference between John and Maria: YJ−YM=−1

Counterfactuals

John Maria
YJ=4 YM=5

This is all the data we actually observe

  • Observed difference between John and Maria: YJ−YM=Y1J−Y0M⏟=−1

  • Recall:

    • John has bought health insurance Y1J
    • Maria has not bought insurance Y0M

  • We don't see the counterfactuals:

    • John's score without insurance
    • Maria score with insurance

Counterfactuals

John Maria
YJ=4 YM=5

This is all the data we actually observe

  • Observed difference between John and Maria: YJ−YM=Y1J−Y0M⏟=−1

  • Algebra trick: add and subtract Y0J to equation

Yj−YM=Y1J−Y0J⏟=1+Y0J−Y0M⏟=−2

  • Y1J−Y0J=1: Causal effect for John of buying insurance, δJ
  • Y0J−Y0M=−2: Difference between John & Maria pre-treatment, “selection bias”

Example II

Y0J−Y0M≠0

  • Selection bias: (pre-existing) differences between members of treatment and control groups other than treatment, that affect the outcome
    • i.e. John and Maria start out with very different health scores before either decides to buy insurance or not (“recieve treatment” or not)

John (Treated)

Maria (Control)

Example II

Y0J−Y0M≠0

  • The choice to get treatment is endogenous

  • A choice made by optimizing agents

  • John and Maria have different preferences, endowments, & constraints that cause them to make different decisions

John (Treated)

Maria (Control)

Example: Our Ideal Data

Ideal (but impossible) Data

Individual Insured Not Insured Diff
John 4.0 3.0 1.0
Maria 5.0 5.0 0.0
Average 4.5 4.0 0.5
  • Individual treatment effect (for individual i): δi=Y1i−Y0i
  • Average treatment effect: ATE=1nn∑i=1(Y1i−Y0i)

Example: Our Ideal Data

Ideal (but impossible) Data

Individual Insured Not Insured Diff
John 4.0 3.0 1.0
Maria 5.0 5.0 0.0
Average 4.5 4.0 0.5
  • Individual treatment effect (for individual i): δi=Y1i−Y0i
  • Average treatment effect: ATE=1nn∑i=1(Y1i−Y0i)

Actual (observed) Data

Individual Insured Not Insured Diff
John 4.0 ? ?
Maria ? 5.0 ?
Average ? ? ?
  • We never get to see each person's counterfactual state to compare and calculate ITEs or ATE
    • Maria with insurance Y1M
    • John without insurance Y0J

Can’t We Just Take the Difference of Group Means?

  • Can’t we just take the difference in group means?

diff.=Avg(Y1i|D=1)−Avg(Y0i|D=0)

Actual (observed) Data

Individual Insured Not Insured Diff
John 4.0 ? ?
Maria ? 5.0 ?
Average ? ? ?
  • We never get to see each person's counterfactual state to compare and calculate ITEs or ATE
    • Maria with insurance Y1M
    • John without insurance Y0J

Can’t We Just Take the Difference of Group Means?

  • Can’t we just take the difference in group means?

diff.=Avg(Y1i|D=1)−Avg(Y0i|D=0)

  • Suppose there is a uniform treatment effect, δi

=Avg(Y1i|D=1)−Avg(Y0i|D=0)=Avg(δi+Y0i|D=1)−Avg(Y0i|D=0)=δi+Avg(Y0i|D=1)−Avg(Y0i|D=0)⏟selection bias=ATE+selection bias

Actual (observed) Data

Individual Insured Not Insured Diff
John 4.0 ? ?
Maria ? 5.0 ?
Average ? ? ?
  • We never get to see each person's counterfactual state to compare and calculate ITEs or ATE
    • Maria with insurance Y1M
    • John without insurance Y0J

Example: Thinking about the Data

  • Basic comparisons tell us something about outcomes, but not ATE

diff.=ATE+Selection Bias

  • Selection bias: difference in average Y0i between groups pre-treatment

  • Y0i includes everything about person i relevant to health except treatment (insurance) status

    • Age, sex, height, weight, climate, smoker, exercise, diet, etc.
    • Imagine a world where nobody gets insurance (treatment), who would have highest health scores?

Actual (observed) Data

Individual Insured Not Insured Diff
John 4.0 ? ?
Maria ? 5.0 ?
Average ? ? ?

Understanding Selection Bias

  • Treatment group and control group differ on average, for reasons other than getting treatment or not!

  • Control group is not a good counterfactual for treatment group without treatment

    • Average untreated outcome for the treatment group differs from average untreated outcome for untreated group

Avg(Y0i|D=1)−Avg(Y0i|D=0)

  • Recall we cannot observe Avg(Y0i|D=1)!

John (Treated)

Maria (Control)

Understanding Selection Bias

  • Consider the problem in regression form:

Y=β0+β1Di+ui

  • Where Di={0 if person is not treated1 if person is treated

  • The problem is cor(D,u)≠0!

    • Di (Treatment) is endogenous!
    • Getting treatment is correlated with other factors that determine health!

John (Treated)

Maria (Control)

Random Assignment: The Silver Bullet

  • If treatment is randomly assigned for a large sample, it eliminates selection bias!

  • Treatment and control groups differ on average by nothing except treatment status

  • Creates ceterus paribus conditions in economics: groups are identical on average (holding constant age, sex, height, etc.)

Treatment Group

Control Group

Random Assignment: The Silver Bullet

  • Consider the problem in regression form:

Y=β0+β1Di+ui

  • If treatment Di is administered randomly, it breaks the correlation with ui!
    • Treatment becomes exogenous
    • cor(D,u)=0

Treatment Group

Control Group

Natural Experiments

The Quest for Causal Effects I

  • RCTs are considered the "gold standard" for causal claims

  • But society is not our laboratory (probably a good thing!)

  • We can rarely conduct experiments to get data

The Quest for Causal Effects II

  • Instead, we often rely on observational data

  • This data is not random!

  • Must take extra care in forming an identification strategy

  • To make good claims about causation in society, we must get clever!

Natural Experiments

  • Economists often resort to searching for natural experiments

  • Some events beyond our control occur that separate otherwise similar entities into a "treatment" group and a "control" group that we can compare

  • e.g. natural disasters, U.S. State laws, military draft

The First Natural Experiment

1813-1858

  • John Snow utilized the first famous natural experiment to establish the foundations of epidemiology and the germ theory of disease

  • Water pumps with sources downstream of a sewage dump in the Thames river spread cholera while water pumps with sources upstream did not

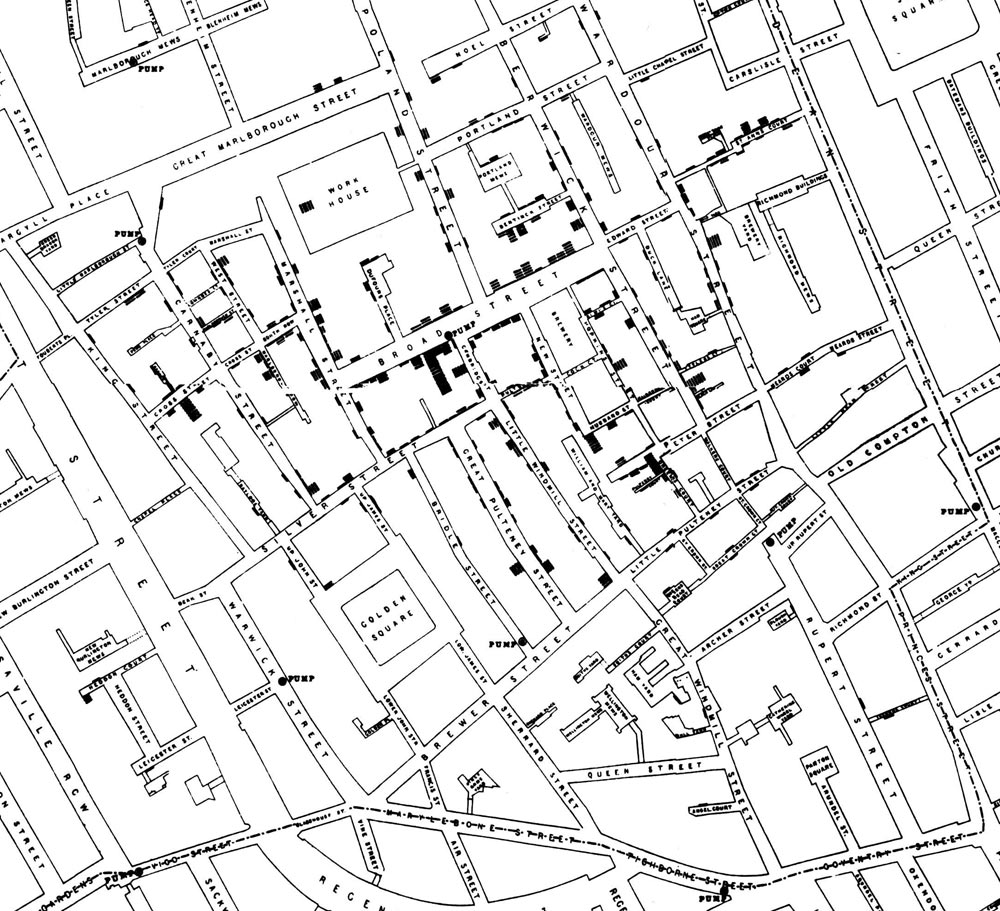
The First Natural Experiment

1813-1858

  • John Snow utilized the first famous natural experiment to establish the foundations of epidemiology and the germ theory of disease

  • Water pumps with sources downstream of a sewage dump in the Thames river spread cholera while water pumps with sources upstream did not

Famous Natural Experiments

  • Oregon Health Insurance Experiment: Oregon used lottery to grant Medicare access to 10,000 people, showing access to Medicaid increased use of health services, lowered debt, etc. relative to those not on Medicaid
  • Angrist (1990) finds that lifetime earnings of (random) drafted Vietnam veterans is 15% lower than non-veterans
  • Card & Kreuger (1994) find that minimum wage hike in fast-food restaurants on NJ side of border had no disemployment effects relative to restaurants on PA side of border during the same period
  • Acemoglu, Johnson, and Robinson (2001) find that inclusive institutions lead to higher economic development than extractive institutions, determined by a colony's disease environment in 1500
  • We will look at some of these in greater detail throughout the course
  • A great list, with explanations is here

Attack of/on the Randomistas

RCTs are All the Rage

Vox (Oct 14, 2019)

But Not Everyone Agrees I

Angus Deaton

Economics Nobel 2015

The RCT is a useful tool, but I think that is a mistake to put method ahead of substance. I have written papers using RCTs...[but] no RCT can ever legitimately claim to have established causality. My theme is that RCTs have no special status, they have no exemption from the problems of inference that econometricians have always wrestled with, and there is nothing that they, and only they, can accomplish.

Deaton, Angus, 2019, “Randomization in the Tropics Revisited: A Theme and Eleven Variations”, Working Paper

But Not Everyone Agrees II

Lant Pritchett

“People keep saying that the recent Nobelists "studied global poverty." This is exactly wrong. They made a commitment to a method, not a subject, and their commitment to method prevented them from studying global poverty.”

“At a conference at Brookings in 2008 Paul Romer (last years Nobelist) said: "You guys are like going to a doctor who says you have an allergy and you have cancer. With the skin rash we can divide you skin into areas and test variety of substances and identify with precision and some certainty the cause. Cancer we have some ideas how to treat it but there are a variety of approaches and since we cannot be sure and precise about which is best for you, we will ignore the cancer and not treat it.”

Source

But Not Everyone Agrees III

Angus Deaton

Economics Nobel 2015

“Lant Pritchett is so fun to listen to, sometimes you could forget that he is completely full of shit.”

Source

RCTs and Evidence-Based Policy

  • Programs randomly assign treatment to different individuals and measure causal effect of treatment

  • RAND Health Insurance Study: randomly give people health insurance

  • Oregon Medicaid Expansion: randomly give people Medicaid

  • HUD's Moving to Opportunity: randomly give people moving vouchers

  • Tennessee STAR: randomly assign students to large vs. small classes

RCTs and External Validity

  • Even if a study is internally valid (used statistics correctly, etc.) we must still worry about external validity:

  • Is the finding generalizable to the whole population?

  • If we find something in India, does that extend to Bolivia? France?

  • Subjects of studies & surveys are often WEIRD: Western, Educated, and from Industrialized Rich Democracies

APA (2010)

RCTs and External Validity

RCTs and External Validity

In Mice twitter account

Outline

First Pass at Causation: RCTs

Potential Outcomes

Natural Experiments

Attack of/on the Randomistas

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow