+ - 0:00:00
Notes for current slide
Notes for next slide

3.9 — Logarithmic Regression

ECON 480 • Econometrics • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF21
metricsF21.classes.ryansafner.com

Outline

Natural Logarithms

Linear-Log Model

Log-Linear Model

Log-Log Model

Comparing Across Units

Joint Hypothesis Testing

Nonlinearities

  • Consider the gapminder example

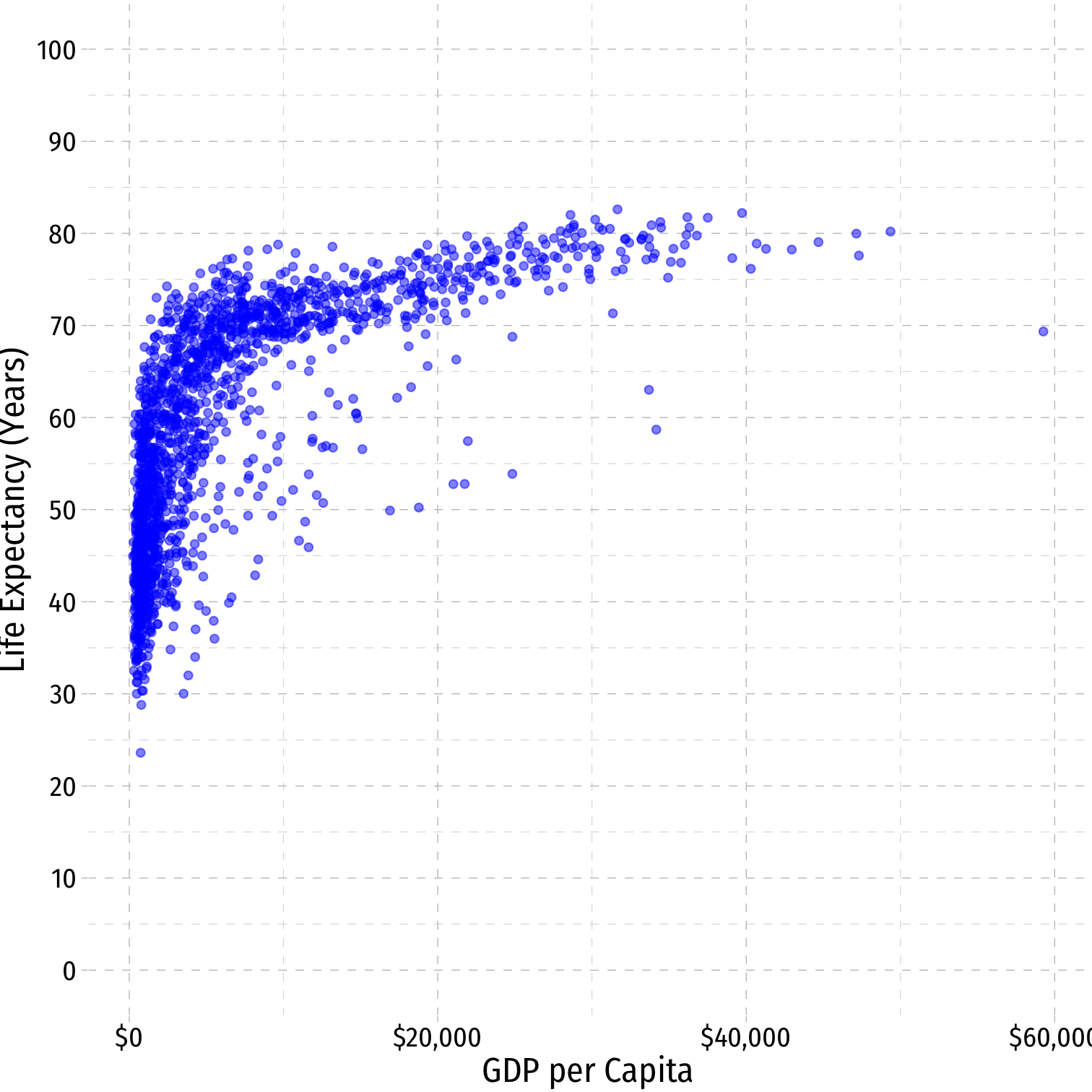
Nonlinearities

  • Consider the gapminder example

^Life Expectancyi=^β0+^β1GDPi

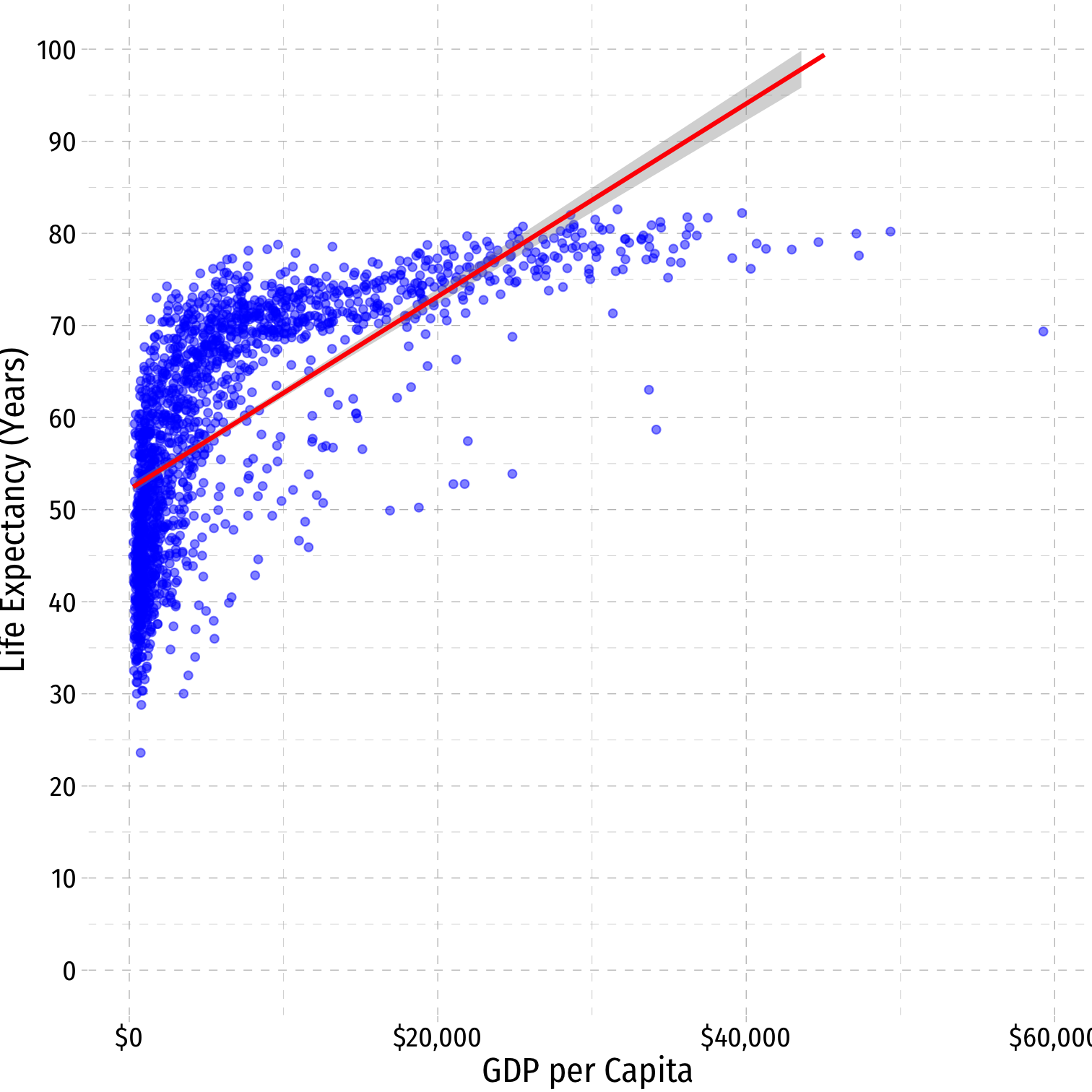
Nonlinearities

  • Consider the gapminder example

^Life Expectancyi=^β0+^β1GDPi

^Life Expectancyi=^β0+^β1GDPi+^β2GDP2i

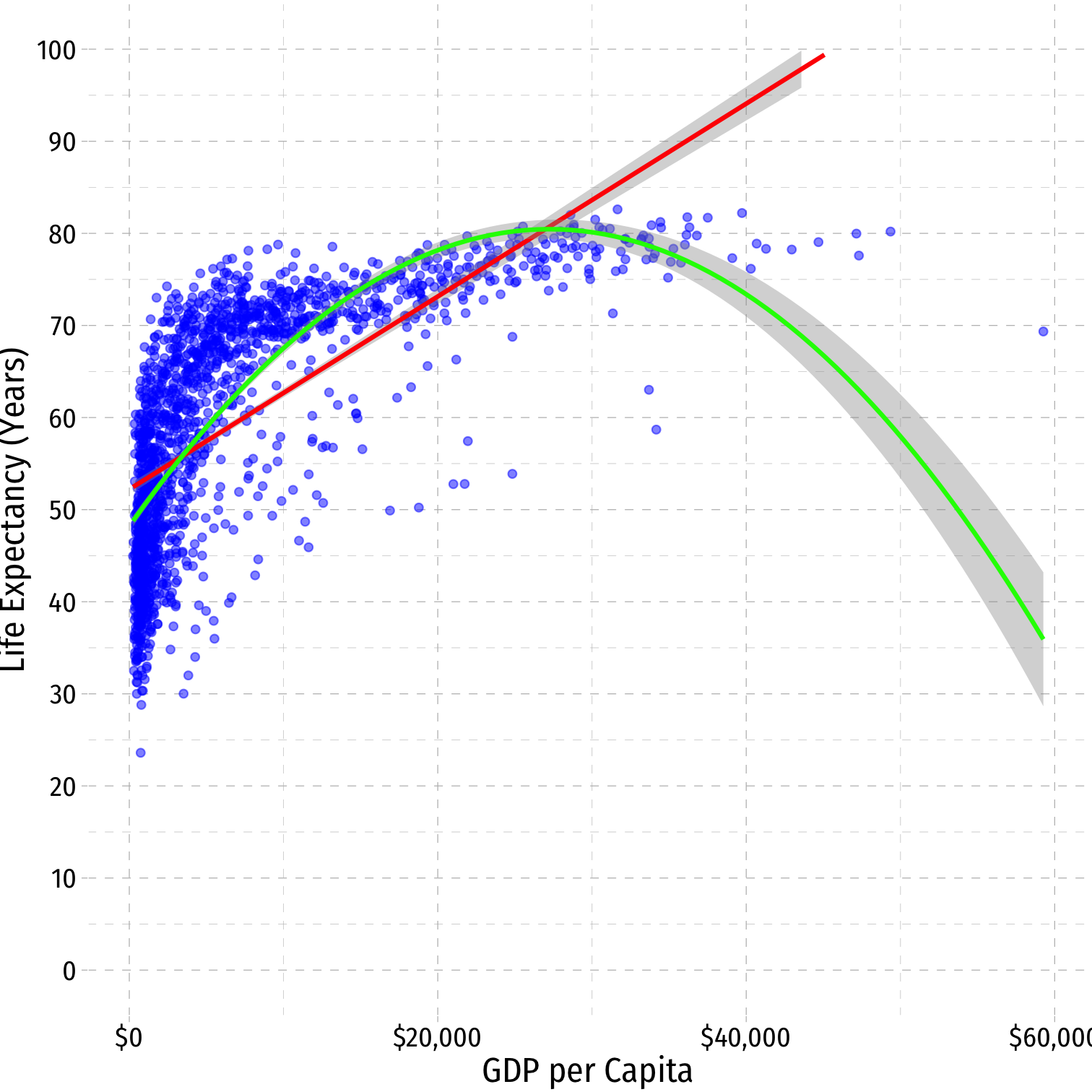
Nonlinearities

  • Consider the gapminder example

^Life Expectancyi=^β0+^β1GDPi

^Life Expectancyi=^β0+^β1GDPi+^β2GDP2i

^Life Expectancyi=^β0+^β1lnGDPi

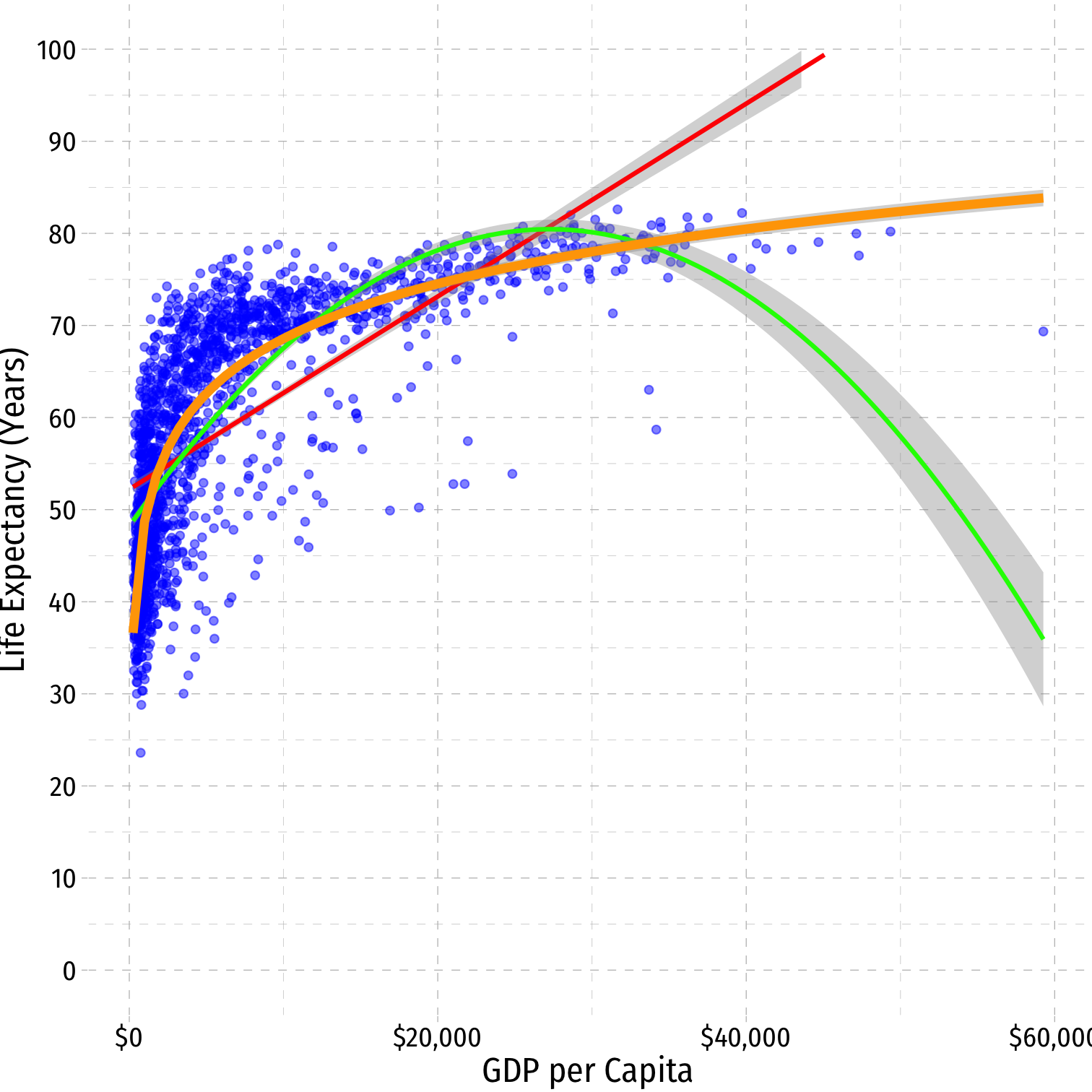
Natural Logarithms

Logarithmic Models

  • Another useful model for nonlinear data is the logarithmic model†

    • We transform either X, Y, or both by taking the (natural) logarithm

  • Logarithmic model has two additional advantages

    1. We can easily interpret coefficients as percentage changes or elasticities
    2. Useful economic shape: diminishing returns (production functions, utility functions, etc)

† Don’t confuse this with a logistic (logit) model for dependent dummy variables.

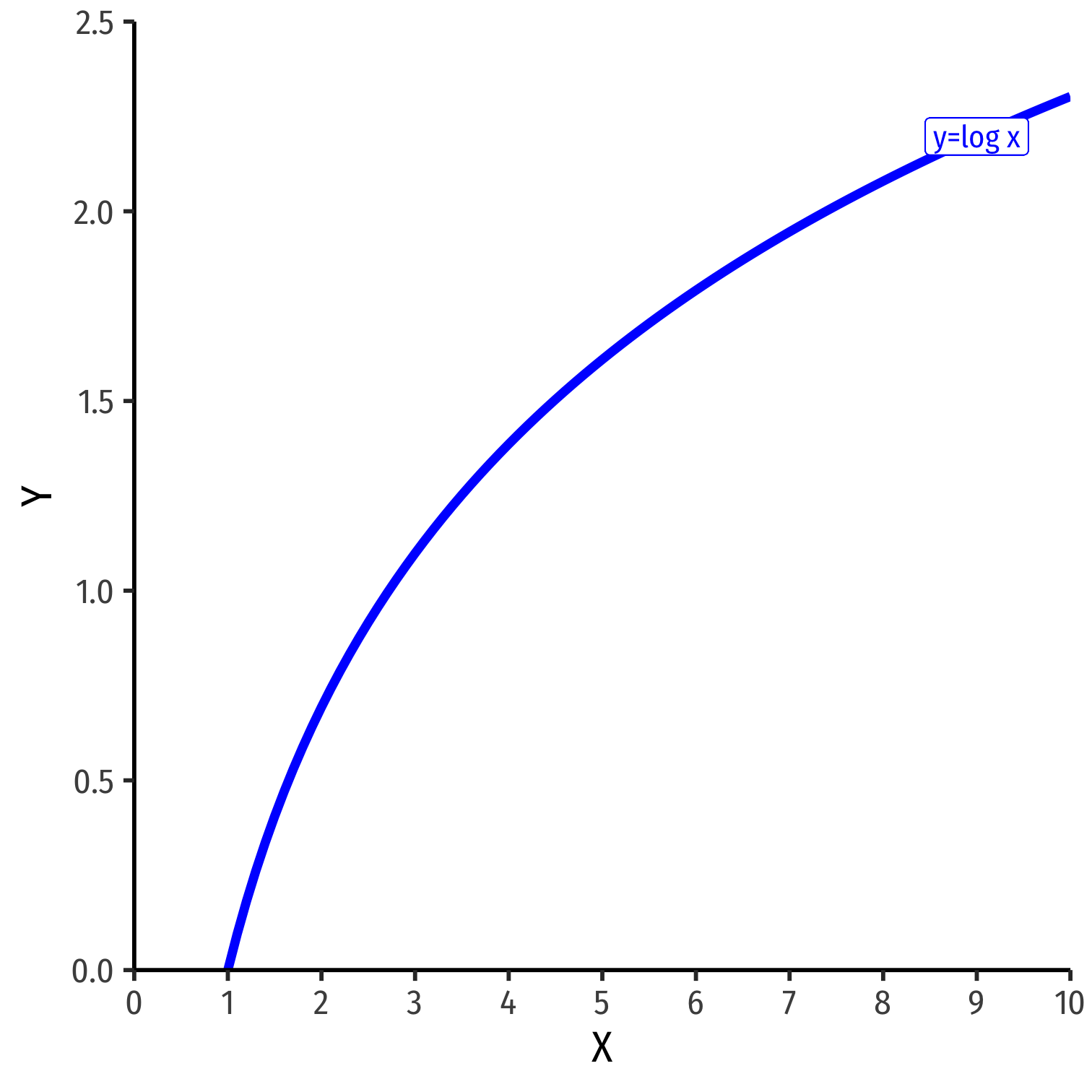
The Natural Logarithm

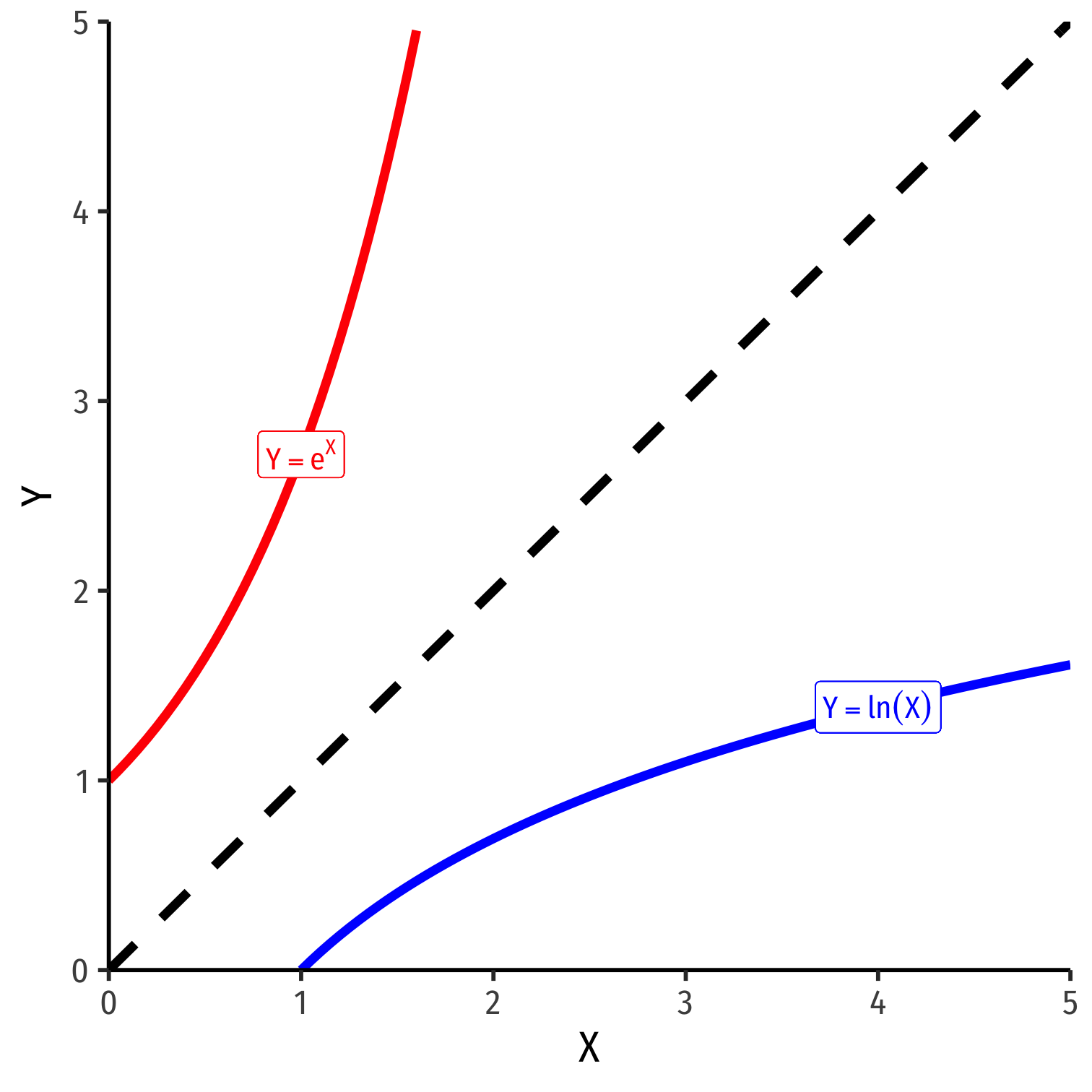
  • The exponential function, Y=eX or Y=exp(X), where base e=2.71828...

  • Natural logarithm is the inverse, Y=ln(X)

The Natural Logarithm: Review I

  • Exponents are defined as bn=b×b×⋯×b⏟n times
    • where base b is multiplied by itself n times

The Natural Logarithm: Review I

  • Exponents are defined as bn=b×b×⋯×b⏟n times
    • where base b is multiplied by itself n times
  • Example: 23=2×2×2⏟n=3=8

The Natural Logarithm: Review I

  • Exponents are defined as bn=b×b×⋯×b⏟n times
    • where base b is multiplied by itself n times
  • Example: 23=2×2×2⏟n=3=8
  • Logarithms are the inverse, defined as the exponents in the expressions above If bn=y, then logb(y)=n
    • n is the number you must raise b to in order to get y

The Natural Logarithm: Review I

  • Exponents are defined as bn=b×b×⋯×b⏟n times
    • where base b is multiplied by itself n times
  • Example: 23=2×2×2⏟n=3=8
  • Logarithms are the inverse, defined as the exponents in the expressions above If bn=y, then logb(y)=n
    • n is the number you must raise b to in order to get y
  • Example: log2(8)=3

The Natural Logarithm: Review II

  • Logarithms can have any base, but common to use the natural logarithm (ln) with base e=2.71828... If en=y, then ln(y)=n

The Natural Logarithm: Properties

  • Natural logs have a lot of useful properties:

  1. ln(1x)=−ln(x)

  2. ln(ab)=ln(a)+ln(b)

  3. ln(xa)=ln(x)−ln(a)

  4. ln(xa)=aln(x)

  5. dlnxdx=1x

The Natural Logarithm: Example

  • Most useful property: for small change in x, Δx:

ln(x+Δx)−ln(x)⏟Difference in logs≈Δxx⏟Relative change

The Natural Logarithm: Example

  • Most useful property: for small change in x, Δx:

ln(x+Δx)−ln(x)⏟Difference in logs≈Δxx⏟Relative change

Example: Let x=100 and Δx=1, relative change is:

Δxx=(101−100)100=0.01 or 1%

  • The logged difference: ln(101)−ln(100)=0.00995≈1%

The Natural Logarithm: Example

  • Most useful property: for small change in x, Δx:

ln(x+Δx)−ln(x)⏟Difference in logs≈Δxx⏟Relative change

Example: Let x=100 and Δx=1, relative change is:

Δxx=(101−100)100=0.01 or 1%

  • The logged difference: ln(101)−ln(100)=0.00995≈1%
  • This allows us to very easily interpret coefficients as percent changes or elasticities

Elasticity

  • An elasticity between any two variables, ϵY,X describes the responsiveness (in %) of one variable (Y) to a change in another (X)

Elasticity

  • An elasticity between any two variables, ϵY,X describes the responsiveness (in %) of one variable (Y) to a change in another (X)

ϵY,X=%ΔY%ΔX=(ΔYY)(ΔXX)

Elasticity

  • An elasticity between any two variables, ϵY,X describes the responsiveness (in %) of one variable (Y) to a change in another (X)

ϵY,X=%ΔY%ΔX=(ΔYY)(ΔXX)

  • Numerator is relative change in Y, Denominator is relative change in X

Elasticity

  • An elasticity between any two variables, ϵY,X describes the responsiveness (in %) of one variable (Y) to a change in another (X)

ϵY,X=%ΔY%ΔX=(ΔYY)(ΔXX)

  • Numerator is relative change in Y, Denominator is relative change in X
  • Interpretation: a 1% change in X will cause a ϵY,X% chang in Y

Math FYI: Cobb Douglas Functions and Logs

  • One of the (many) reasons why economists love Cobb-Douglas functions: Y=ALαKβ

Math FYI: Cobb Douglas Functions and Logs

  • One of the (many) reasons why economists love Cobb-Douglas functions: Y=ALαKβ

  • Taking logs, relationship becomes linear:

Math FYI: Cobb Douglas Functions and Logs

  • One of the (many) reasons why economists love Cobb-Douglas functions: Y=ALαKβ

  • Taking logs, relationship becomes linear:

ln(Y)=ln(A)+αln(L)+βln(K)

Math FYI: Cobb Douglas Functions and Logs

  • One of the (many) reasons why economists love Cobb-Douglas functions: Y=ALαKβ

  • Taking logs, relationship becomes linear:

ln(Y)=ln(A)+αln(L)+βln(K)

  • With data on (Y,L,K) and linear regression, can estimate α and β
    • α: elasticity of Y with respect to L
      • A 1% change in L will lead to an α% change in Y
    • β: elasticity of Y with respect to K
      • A 1% change in K will lead to a β% change in Y

Math FYI: Cobb Douglas Functions and Logs

Example: Cobb-Douglas production function: Y=2L0.75K0.25

Math FYI: Cobb Douglas Functions and Logs

Example: Cobb-Douglas production function: Y=2L0.75K0.25

  • Taking logs:

lnY=ln2+0.75lnL+0.25lnK

Math FYI: Cobb Douglas Functions and Logs

Example: Cobb-Douglas production function: Y=2L0.75K0.25

  • Taking logs:

lnY=ln2+0.75lnL+0.25lnK

  • A 1% change in L will yield a 0.75% change in output Y

  • A 1% change in K will yield a 0.25% change in output Y

Logarithms in R I

  • The log() function can easily take the logarithm
gapminder <- gapminder %>%
  mutate(loggdp = log(gdpPercap)) # log GDP per capita
gapminder %>% head() # look at it
ABCDEFGHIJ0123456789
country
<fct>
continent
<fct>
year
<int>
lifeExp
<dbl>
pop
<int>
gdpPercap
<dbl>
loggdp
<dbl>
AfghanistanAsia195228.8018425333779.44536.658583
AfghanistanAsia195730.3329240934820.85306.710344
AfghanistanAsia196231.99710267083853.10076.748878
AfghanistanAsia196734.02011537966836.19716.728864
AfghanistanAsia197236.08813079460739.98116.606625
AfghanistanAsia197738.43814880372786.11346.667101
6 rows

Logarithms in R II

  • Note, log() by default is the natural logarithm ln(), i.e. base e
    • Can change base with e.g. log(x, base = 5)
    • Some common built-in logs: log10, log2 
log10(100)
## [1] 2
log2(16)
## [1] 4
log(19683, base=3)
## [1] 9

Logarithms in R III

  • Note when running a regression, you can pre-transform the data into logs (as I did above), or just add log() around a variable in the regression
lm(lifeExp ~ loggdp,
   data = gapminder) %>%
  tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
loggdp8.4050850.14876256.500206
2 rows | 1-4 of 5 columns
lm(lifeExp ~ log(gdpPercap),
   data = gapminder) %>%
  tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
log(gdpPercap)8.4050850.14876256.500206
2 rows | 1-4 of 5 columns

Types of Logarithmic Models

  • Three types of log regression models, depending on which variables we log

Types of Logarithmic Models

  • Three types of log regression models, depending on which variables we log
  1. Linear-log model: Yi=β0+β1lnXi

Types of Logarithmic Models

  • Three types of log regression models, depending on which variables we log

  1. Linear-log model: Yi=β0+β1lnXi

  2. Log-linear model: lnYi=β0+β1Xi

Types of Logarithmic Models

  • Three types of log regression models, depending on which variables we log

  1. Linear-log model: Yi=β0+β1lnXi

  2. Log-linear model: lnYi=β0+β1Xi

  3. Log-log model: lnYi=β0+β1lnXi

Linear-Log Model

Linear-Log Model

  • Linear-log model has an independent variable (X) that is logged

Linear-Log Model

  • Linear-log model has an independent variable (X) that is logged

Y=β0+β1lnXiβ1=ΔY(ΔXX)

Linear-Log Model

  • Linear-log model has an independent variable (X) that is logged

Y=β0+β1lnXiβ1=ΔY(ΔXX)

  • Marginal effect of X→Y: a 1% change in X→ a β1100 unit change in Y

Linear-Log Model in R

lin_log_reg <- lm(lifeExp ~ loggdp,
                  data = gapminder)
library(broom)
lin_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
loggdp8.4050850.14876256.500206
2 rows | 1-4 of 5 columns

^Life Expectancyi=−9.10+8.41ln GDPi

Linear-Log Model in R

lin_log_reg <- lm(lifeExp ~ loggdp,
                  data = gapminder)
library(broom)
lin_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
loggdp8.4050850.14876256.500206
2 rows | 1-4 of 5 columns

^Life Expectancyi=−9.10+8.41ln GDPi

  • A 1% change in GDP → a 9.41100= 0.0841 year increase in Life Expectancy

Linear-Log Model in R

lin_log_reg <- lm(lifeExp ~ loggdp,
                  data = gapminder)
library(broom)
lin_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
loggdp8.4050850.14876256.500206
2 rows | 1-4 of 5 columns

^Life Expectancyi=−9.10+8.41ln GDPi

  • A 1% change in GDP → a 9.41100= 0.0841 year increase in Life Expectancy

  • A 25% fall in GDP → a (−25×0.0841)= 2.1025 year decrease in Life Expectancy

Linear-Log Model in R

lin_log_reg <- lm(lifeExp ~ loggdp,
                  data = gapminder)
library(broom)
lin_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)-9.1008891.227674-7.413117
loggdp8.4050850.14876256.500206
2 rows | 1-4 of 5 columns

^Life Expectancyi=−9.10+8.41ln GDPi

  • A 1% change in GDP → a 9.41100= 0.0841 year increase in Life Expectancy

  • A 25% fall in GDP → a (−25×0.0841)= 2.1025 year decrease in Life Expectancy

  • A 100% rise in GDP → a (100×0.0841)= 8.4100 year increase in Life Expectancy

Linear-Log Model Graph I

ggplot(data = gapminder)+
  aes(x = gdpPercap,
      y = lifeExp)+
  geom_point(color="blue", alpha=0.5)+
  geom_smooth(method="lm",
              formula=y~log(x),
              color="orange")+
  scale_x_continuous(labels=scales::dollar,
                     breaks=seq(0,120000,20000))+
  scale_y_continuous(breaks=seq(0,100,10),
                     limits=c(0,100))+
  labs(x = "GDP per Capita",
       y = "Life Expectancy (Years)")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed",
           base_size=16)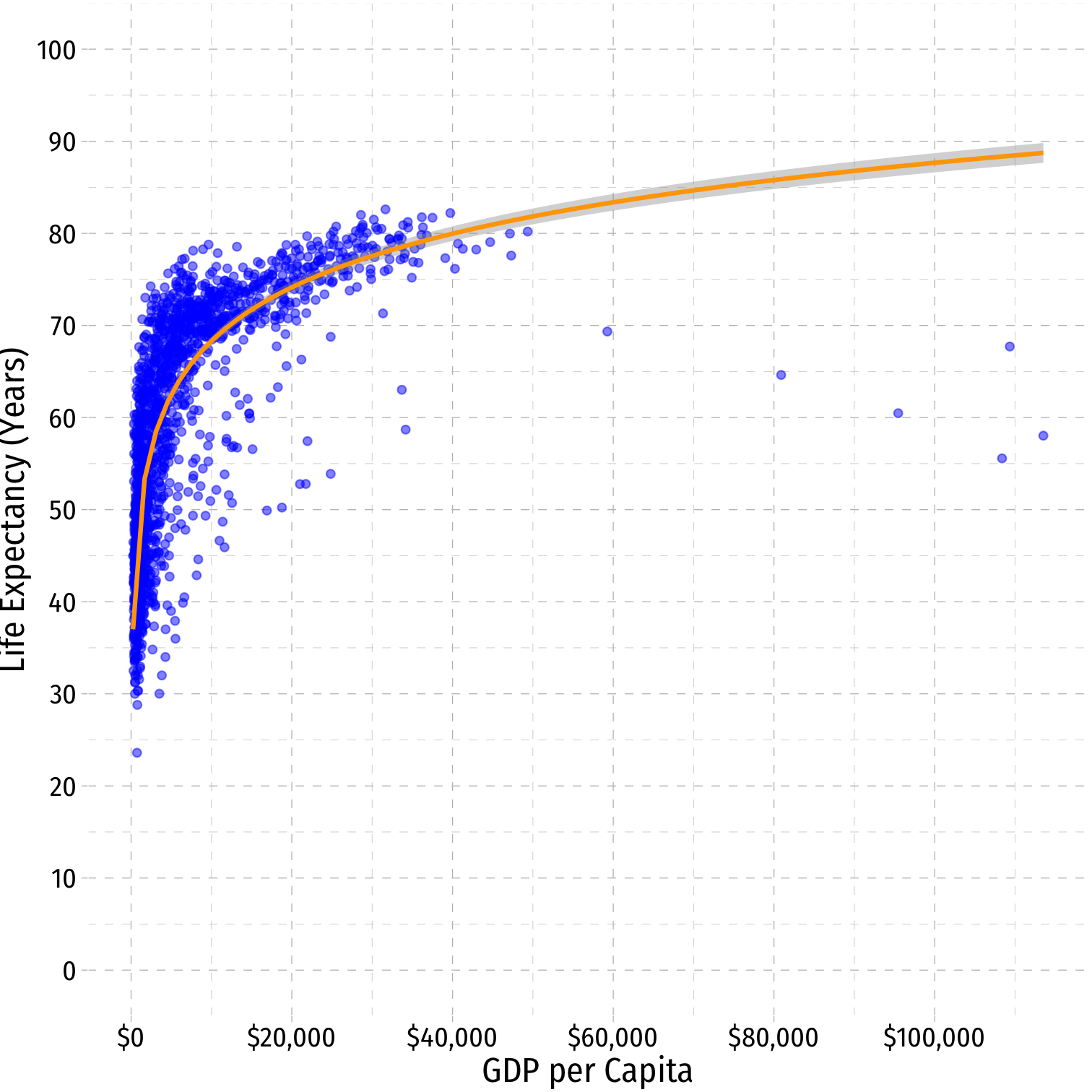

Linear-Log Model Graph II

ggplot(data = gapminder)+
  aes(x = loggdp,
      y = lifeExp)+ 
  geom_point(color="blue", alpha=0.5)+
  geom_smooth(method="lm", color="orange")+
  scale_y_continuous(breaks=seq(0,100,10),
                     limits=c(0,100))+
  labs(x = "Log GDP per Capita",
       y = "Life Expectancy (Years)")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed",
           base_size=16)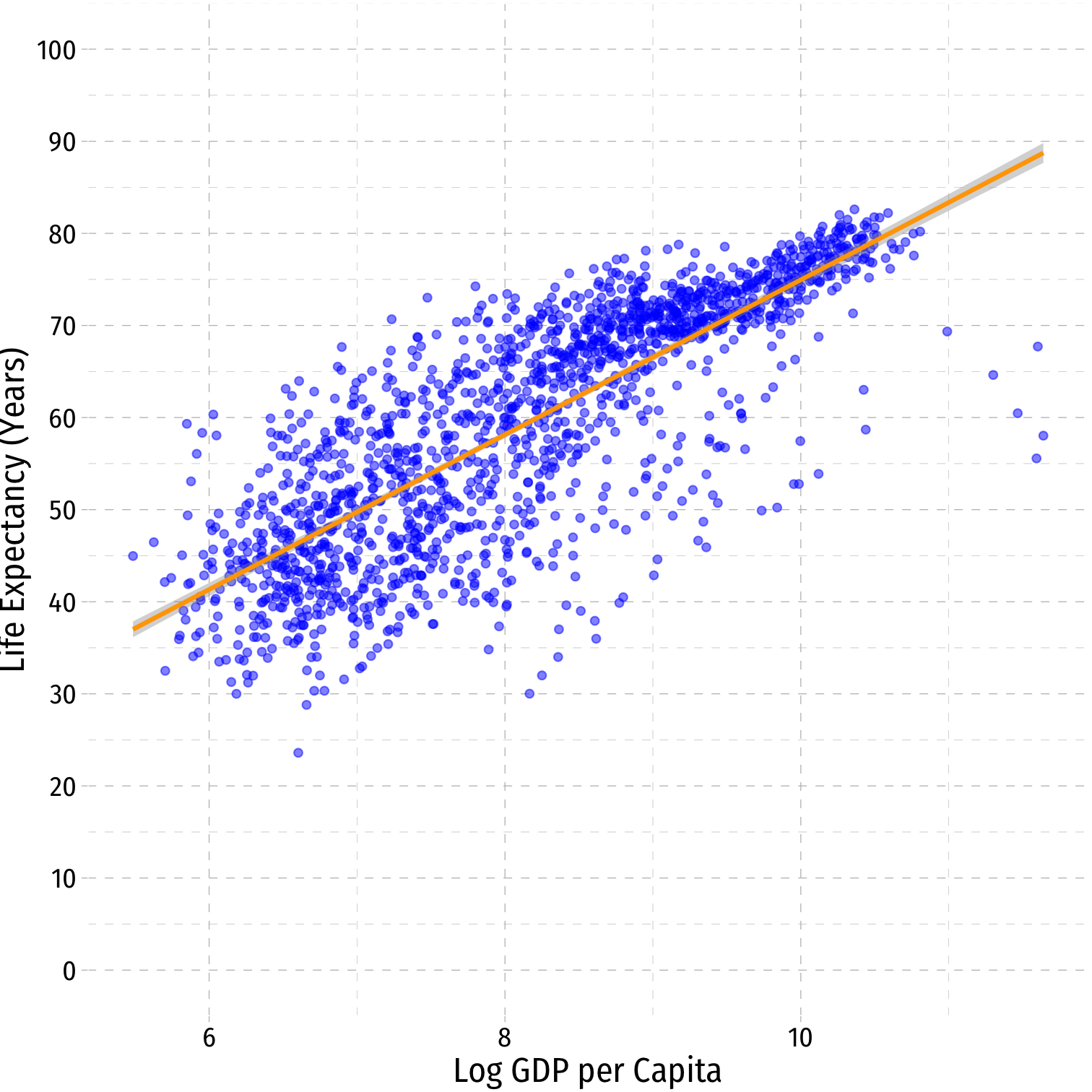

Log-Linear Model

Log-Linear Model

  • Log-linear model has the dependent variable (Y) logged

Log-Linear Model

  • Log-linear model has the dependent variable (Y) logged

lnYi=β0+β1Xβ1=(ΔYY)ΔX

Log-Linear Model

  • Log-linear model has the dependent variable (Y) logged

lnYi=β0+β1Xβ1=(ΔYY)ΔX

  • Marginal effect of X→Y: a 1 unit change in X→ a β1×100 % change in Y

Log-Linear Model in R (Preliminaries)

  • We will again have very large/small coefficients if we deal with GDP directly, again let's transform gdpPercap into $1,000s, call it gdp_t

  • Then log LifeExp

Log-Linear Model in R (Preliminaries)

  • We will again have very large/small coefficients if we deal with GDP directly, again let's transform gdpPercap into $1,000s, call it gdp_t

  • Then log LifeExp

gapminder <- gapminder %>%
  mutate(gdp_t = gdpPercap/1000, # first make GDP/capita in $1000s
         loglife = log(lifeExp)) # take the log of LifeExp
gapminder %>% head() # look at it
ABCDEFGHIJ0123456789
country
<fct>
continent
<fct>
year
<int>
lifeExp
<dbl>
pop
<int>
gdpPercap
<dbl>
loggdp
<dbl>
gdp_t
<dbl>
loglife
<dbl>
AfghanistanAsia195228.8018425333779.44536.6585830.77944533.360410
AfghanistanAsia195730.3329240934820.85306.7103440.82085303.412203
AfghanistanAsia196231.99710267083853.10076.7488780.85310073.465642
AfghanistanAsia196734.02011537966836.19716.7288640.83619713.526949
AfghanistanAsia197236.08813079460739.98116.6066250.73998113.585960
AfghanistanAsia197738.43814880372786.11346.6671010.78611343.649047
6 rows

Log-Linear Model in R

log_lin_reg <- lm(loglife~gdp_t,
                data = gapminder)
log_lin_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)3.9666390.0058345501679.85339
gdp_t0.0129170.000477707227.03958
2 rows | 1-4 of 5 columns

^lnLife Expectancyi=3.967+0.013GDPi

Log-Linear Model in R

log_lin_reg <- lm(loglife~gdp_t,
                data = gapminder)
log_lin_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)3.9666390.0058345501679.85339
gdp_t0.0129170.000477707227.03958
2 rows | 1-4 of 5 columns

^lnLife Expectancyi=3.967+0.013GDPi

  • A $1 (thousand) change in GDP → a 0.013×100%= 1.3% increase in Life Expectancy

Log-Linear Model in R

log_lin_reg <- lm(loglife~gdp_t,
                data = gapminder)
log_lin_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)3.9666390.0058345501679.85339
gdp_t0.0129170.000477707227.03958
2 rows | 1-4 of 5 columns

^ln(Life Expectancy)i=3.967+0.013GDPi

  • A $1 (thousand) change in GDP → a 0.013×100%= 1.3% increase in Life Expectancy

  • A $25 (thousand) fall in GDP → a (−25×1.3%)= 32.5% decrease in Life Expectancy

Log-Linear Model in R

log_lin_reg <- lm(loglife~gdp_t,
                data = gapminder)
log_lin_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)3.9666390.0058345501679.85339
gdp_t0.0129170.000477707227.03958
2 rows | 1-4 of 5 columns

^ln(Life Expectancy)i=3.967+0.013GDPi

  • A $1 (thousand) change in GDP → a 0.013×100%= 1.3% increase in Life Expectancy

  • A $25 (thousand) fall in GDP → a (−25×1.3%)= 32.5% decrease in Life Expectancy

  • A $100 (thousand) rise in GDP → a (100×1.3%)= 130% increase in Life Expectancy

Linear-Log Model Graph I

ggplot(data = gapminder)+
  aes(x = gdp_t,
      y = loglife)+
  geom_point(color="blue", alpha=0.5)+
  geom_smooth(method="lm", color="orange")+
  scale_x_continuous(labels=scales::dollar,
                     breaks=seq(0,120,20))+
  labs(x = "GDP per Capita ($ Thousands)",
       y = "Log Life Expectancy")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed",
           base_size=16)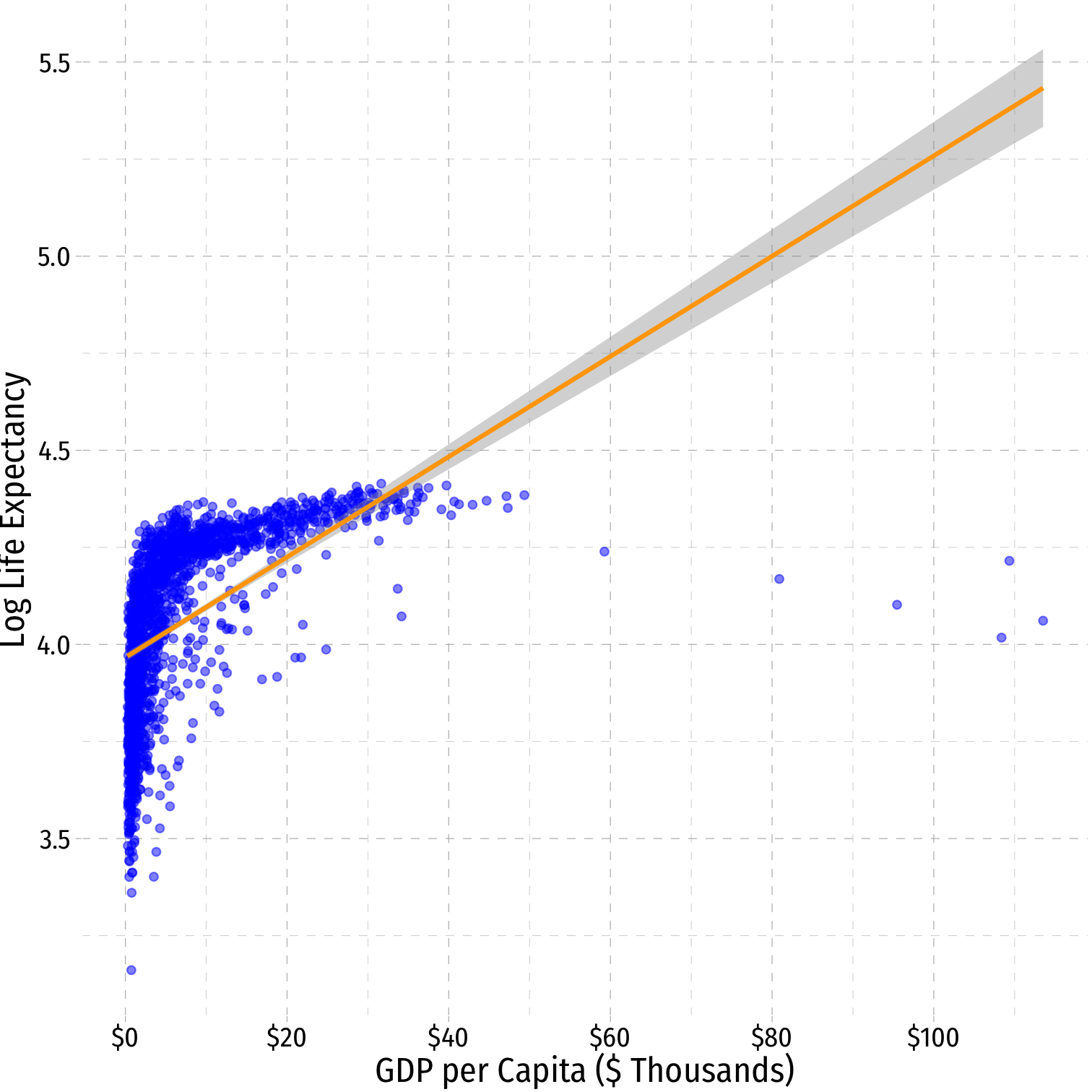

Log-Log Model

Log-Log Model

  • Log-log model has both variables (X and Y) logged

Log-Log Model

  • Log-log model has both variables (X and Y) logged

lnYi=β0+β1lnXiβ1=(ΔYY)(ΔXX)

Log-Log Model

  • Log-log model has both variables (X and Y) logged

lnYi=β0+β1lnXiβ1=(ΔYY)(ΔXX)

  • Marginal effect of X→Y: a 1% change in X→ a β1 % change in Y

  • β1 is the elasticity of Y with respect to X!

Log-Log Model in R

log_log_reg <- lm(loglife ~ loggdp,
                  data = gapminder)
log_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)2.8641770.02328274123.017180
loggdp0.1465490.0028212651.944520
2 rows

^ln Life Expectancyi=2.864+0.147ln GDPi

Log-Log Model in R

log_log_reg <- lm(loglife ~ loggdp,
                  data = gapminder)
log_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)2.8641770.02328274123.017180
loggdp0.1465490.0028212651.944520
2 rows

^ln Life Expectancyi=2.864+0.147ln GDPi

  • A 1% change in GDP → a 0.147% increase in Life Expectancy

Log-Log Model in R

log_log_reg <- lm(loglife ~ loggdp,
                  data = gapminder)
log_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)2.8641770.02328274123.017180
loggdp0.1465490.0028212651.944520
2 rows

^ln Life Expectancyi=2.864+0.147ln GDPi

  • A 1% change in GDP → a 0.147% increase in Life Expectancy

  • A 25% fall in GDP → a (−25×0.147%)= 3.675% decrease in Life Expectancy

Log-Log Model in R

log_log_reg <- lm(loglife ~ loggdp,
                  data = gapminder)
log_log_reg %>% tidy()
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
p.value
<dbl>
(Intercept)2.8641770.02328274123.017180
loggdp0.1465490.0028212651.944520
2 rows

^ln Life Expectancyi=2.864+0.147ln GDPi

  • A 1% change in GDP → a 0.147% increase in Life Expectancy

  • A 25% fall in GDP → a (−25×0.147%)= 3.675% decrease in Life Expectancy

  • A 100% rise in GDP → a (100×0.147%)= 14.7% increase in Life Expectancy

Log-Log Model Graph I

ggplot(data = gapminder)+
  aes(x = loggdp,
      y = loglife)+
  geom_point(color="blue", alpha=0.5)+
  geom_smooth(method="lm", color="orange")+
  labs(x = "Log GDP per Capita",
       y = "Log Life Expectancy")+
  ggthemes::theme_pander(base_family = "Fira Sans Condensed",
           base_size=16)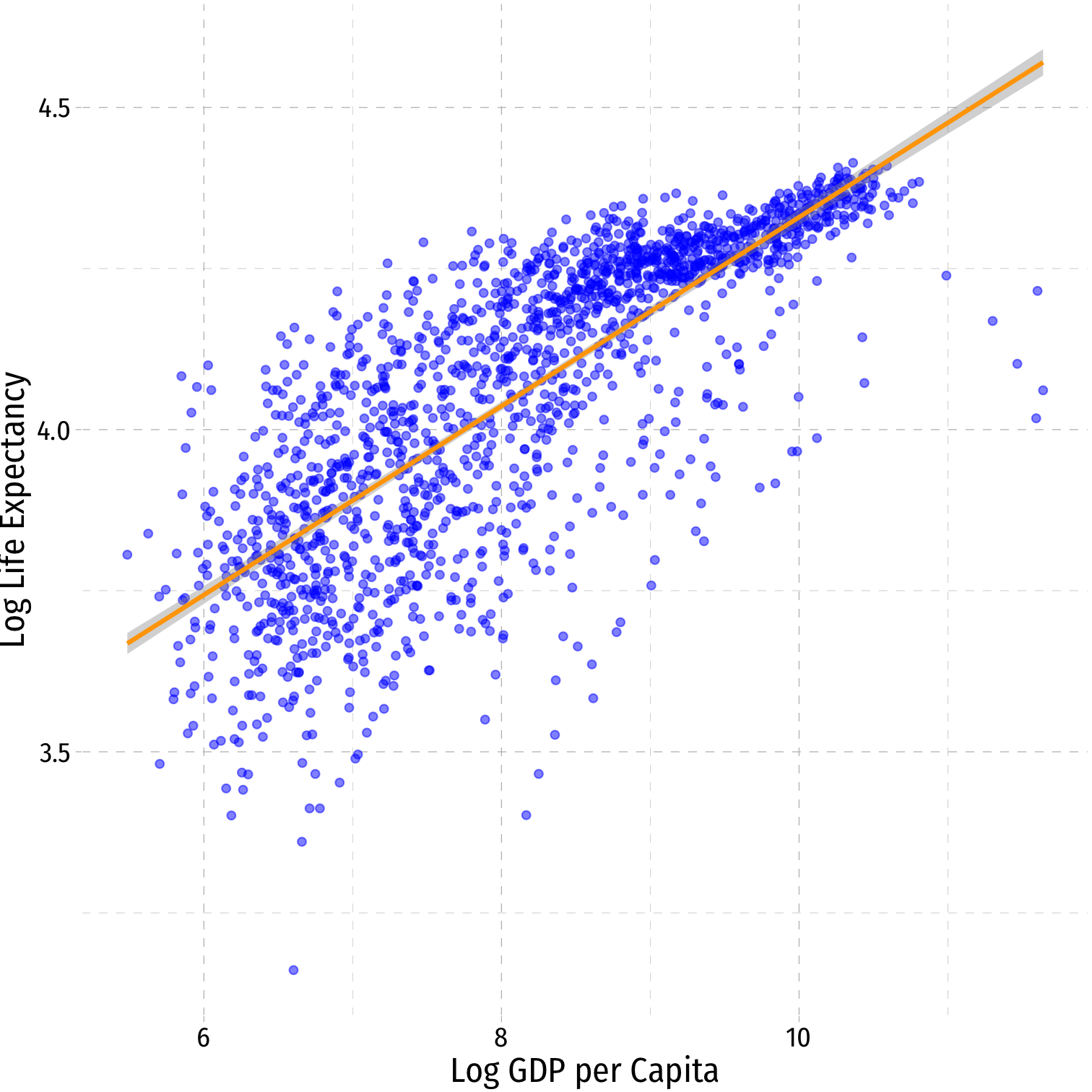

Comparing Models I

Model Equation Interpretation
Linear-Log Y=β0+β1lnX 1% change in X→^β1100 unit change in Y
Log-Linear lnY=β0+β1X 1 unit change in X→^β1×100% change in Y
Log-Log lnY=β0+β1lnX 1% change in X→^β1% change in Y
  • Hint: the variable that gets logged changes in percent terms, the variable not logged changes in unit terms
    • Going from units → percent: multiply by 100
    • Going from percent → units: divide by 100

Comparing Models II

library(huxtable)
huxreg("Life Exp." = lin_log_reg,
       "Log Life Exp." = log_lin_reg,
       "Log Life Exp." = log_log_reg,
       coefs = c("Constant" = "(Intercept)",
                 "GDP ($1000s)" = "gdp_t",
                 "Log GDP" = "loggdp"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 2)
  • Models are very different units, how to choose?
    • Compare R2’s
    • Compare graphs
    • Compare intution
Life Exp.Log Life Exp.Log Life Exp.
Constant-9.10 ***3.97 ***2.86 ***
(1.23)   (0.01)   (0.02)   
GDP ($1000s)       0.01 ***       
       (0.00)          
Log GDP8.41 ***       0.15 ***
(0.15)          (0.00)   
N1704       1704       1704       
R-Squared0.65    0.30    0.61    
SER7.62    0.19    0.14    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Comparing Models III

Linear-Log Log-Linear Log-Log
^Yi=^β0+^β1lnXi lnYi=^β0+^β1Xi lnYi=^β0+^β1lnXi
R2=0.65 R2=0.30 R2=0.61

When to Log?

  • In practice, the following types of variables are logged:
    • Variables that must always be positive (prices, sales, market values)
    • Very large numbers (population, GDP)
    • Variables we want to talk about as percentage changes or growth rates (money supply, population, GDP)
    • Variables that have diminishing returns (output, utility)
    • Variables that have nonlinear scatterplots

When to Log?

  • In practice, the following types of variables are logged:
    • Variables that must always be positive (prices, sales, market values)
    • Very large numbers (population, GDP)
    • Variables we want to talk about as percentage changes or growth rates (money supply, population, GDP)
    • Variables that have diminishing returns (output, utility)
    • Variables that have nonlinear scatterplots
  • Avoid logs for:
    • Variables that are less than one, decimals, 0, or negative
    • Categorical variables (season, gender, political party)
    • Time variables (year, week, day)

Comparing Across Units

Comparing Coefficients of Different Units I

^Yi=β0+β1X1+β2X2

  • We often want to compare coefficients to see which variable X1 or X2 has a bigger effect on Y

  • What if X1 and X2 are different units?

Example: ^Salaryi=β0+β1Batting averagei+β2Home runsi^Salaryi=−2,869,439.40+12,417,629.72Batting averagei+129,627.36Home runsi

Comparing Coefficients of Different Units II

  • An easy way is to standardize† the variables (i.e. take the Z-score)

XZ=Xi−¯Xsd(X)

† Also called “centering” or “scaling.”

Comparing Coefficients of Different Units: Example

Variable Mean Std. Dev.
Salary $2,024,616 $2,764,512
Batting Average 0.267 0.031
Home Runs 12.11 10.31

^Salaryi=−2,869,439.40+12,417,629.72Batting averagei+129,627.36Home runsi^SalaryZ=0.00+0.14Batting averageZ+0.48Home runsZ

Comparing Coefficients of Different Units: Example

Variable Mean Std. Dev.
Salary $2,024,616 $2,764,512
Batting Average 0.267 0.031
Home Runs 12.11 10.31

^Salaryi=−2,869,439.40+12,417,629.72Batting averagei+129,627.36Home runsi^SalaryZ=0.00+0.14Batting averageZ+0.48Home runsZ

  • Marginal effects on Y (in standard deviations of Y) from 1 standard deviation change in X:

  • ^β1: a 1 standard deviation increase in Batting Average increases Salary by 0.14 standard deviations

0.14×$2,764,512=$387,032

  • ^β2: a 1 standard deviation increase in Home Runs increases Salary by 0.48 standard deviations

0.48×$2,764,512=$1,326,966

Standardizing in R

Variable Mean SD
LifeExp 59.47 12.92
gdpPercap $7215.32 $9857.46
  • Use the scale() command inside mutate() function to standardize a variable
gapminder <- gapminder %>%
  mutate(life_Z = scale(lifeExp),
         gdp_Z = scale(gdpPercap))
std_reg <- lm(life_Z ~ gdp_Z, data = gapminder)
tidy(std_reg)
## # A tibble: 2 × 5
##   term        estimate std.error statistic   p.value
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept) 1.10e-16    0.0197  5.57e-15 1.00e+  0
## 2 gdp_Z       5.84e- 1    0.0197  2.97e+ 1 3.57e-156
  • A 1 standard deviation increase in gdpPercap will increase lifeExp by 0.584 standard deviations (0.584×12.92==7.55 years)

Joint Hypothesis Testing

Joint Hypothesis Testing I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

Joint Hypothesis Testing I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Maybe region doesn't affect wages at all?

Joint Hypothesis Testing I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Maybe region doesn't affect wages at all?

  • H0:β2=0,β3=0,β4=0

Joint Hypothesis Testing I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Maybe region doesn't affect wages at all?

  • H0:β2=0,β3=0,β4=0

  • This is a joint hypothesis to test

Joint Hypothesis Testing II

  • A joint hypothesis tests against the null hypothesis of a value for multiple parameters: H0:β1=β2=0
    the hypotheses that multiple regressors are equal to zero (have no causal effect on the outcome)

Joint Hypothesis Testing II

  • A joint hypothesis tests against the null hypothesis of a value for multiple parameters: H0:β1=β2=0

    the hypotheses that multiple regressors are equal to zero (have no causal effect on the outcome)

  • Our alternative hypothesis is that: H1: either β1≠0 or β2≠0 or both

    or simply, that H0 is not true

Types of Joint Hypothesis Tests

1) H0: β1=β2=0

  • Testing against the claim that multiple variables don't matter
  • Useful under high multicollinearity between variables
  • Ha: at least one parameter ≠ 0

Types of Joint Hypothesis Tests

1) H0: β1=β2=0

  • Testing against the claim that multiple variables don't matter
  • Useful under high multicollinearity between variables
  • Ha: at least one parameter ≠ 0

2) H0: β1=β2

  • Testing whether two variables matter the same
  • Variables must be the same units
  • Ha:β1(≠,<, or >)β2

Types of Joint Hypothesis Tests

1) H0: β1=β2=0

  • Testing against the claim that multiple variables don't matter
  • Useful under high multicollinearity between variables
  • Ha: at least one parameter ≠ 0

2) H0: β1=β2

  • Testing whether two variables matter the same
  • Variables must be the same units
  • Ha:β1(≠,<, or >)β2

3) H0: ALL β's =0

  • The "Overall F-test"
  • Testing against claim that regression model explains NO variation in Y

Joint Hypothesis Tests: F-statistic

  • The F-statistic is the test-statistic used to test joint hypotheses about regression coefficients with an F-test

Joint Hypothesis Tests: F-statistic

  • The F-statistic is the test-statistic used to test joint hypotheses about regression coefficients with an F-test

  • This involves comparing two models:

    1. Unrestricted model: regression with all coefficients
    2. Restricted model: regression under null hypothesis (coefficients equal hypothesized values)

Joint Hypothesis Tests: F-statistic

  • The F-statistic is the test-statistic used to test joint hypotheses about regression coefficients with an F-test

  • This involves comparing two models:

    1. Unrestricted model: regression with all coefficients
    2. Restricted model: regression under null hypothesis (coefficients equal hypothesized values)

  • F is an analysis of variance (ANOVA)

    • essentially tests whether R2 increases statistically significantly as we go from the restricted model$\rightarrow$unrestricted model

Joint Hypothesis Tests: F-statistic

  • The F-statistic is the test-statistic used to test joint hypotheses about regression coefficients with an F-test

  • This involves comparing two models:

    1. Unrestricted model: regression with all coefficients
    2. Restricted model: regression under null hypothesis (coefficients equal hypothesized values)

  • F is an analysis of variance (ANOVA)

    • essentially tests whether R2 increases statistically significantly as we go from the restricted model$\rightarrow$unrestricted model

  • F has its own distribution, with two sets of degrees of freedom

Joint Hypothesis F-test: Example I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

Joint Hypothesis F-test: Example I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • H0:β2=β3=β4=0

Joint Hypothesis F-test: Example I

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • H0:β2=β3=β4=0

  • Ha: H0 is not true (at least one βi≠0)

Joint Hypothesis F-test: Example II

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Unrestricted model:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

Joint Hypothesis F-test: Example II

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Unrestricted model:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Restricted model:

^Wagei=^β0+^β1Malei

Joint Hypothesis F-test: Example II

Example: Return again to:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Unrestricted model:

^Wagei=^β0+^β1Malei+^β2Northeasti+^β3Midwesti+^β4Southi

  • Restricted model:

^Wagei=^β0+^β1Malei

  • F-test: does going from restricted to unrestricted model statistically significantly improve R2?

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • R2u: the R2 from the unrestricted model (all variables)

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • R2u: the R2 from the unrestricted model (all variables)

  • R2r: the R2 from the restricted model (null hypothesis)

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • R2u: the R2 from the unrestricted model (all variables)

  • R2r: the R2 from the restricted model (null hypothesis)

  • q: number of restrictions (number of β′s=0 under null hypothesis)

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • R2u: the R2 from the unrestricted model (all variables)

  • R2r: the R2 from the restricted model (null hypothesis)

  • q: number of restrictions (number of β′s=0 under null hypothesis)

  • k: number of X variables in unrestricted model (all variables)

Calculating the F-statistic

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • R2u: the R2 from the unrestricted model (all variables)

  • R2r: the R2 from the restricted model (null hypothesis)

  • q: number of restrictions (number of β′s=0 under null hypothesis)

  • k: number of X variables in unrestricted model (all variables)

  • F has two sets of degrees of freedom:

    • q for the numerator, (n−k−1) for the denominator

Calculating the F-statistic II

Fq,(n−k−1)=((R2u−R2r)q)((1−R2u)(n−k−1))

  • Key takeaway: The bigger the difference between (R2u−R2r), the greater the improvement in fit by adding variables, the larger the F!

  • This formula is (believe it or not) actually a simplified version (assuming homoskedasticity)

    • I give you this formula to build your intuition of what F is measuring

F-test Example I

  • We'll use the wooldridge package's wage1 data again
# load in data from wooldridge package
library(wooldridge)
wages <- wage1
# run regressions
unrestricted_reg <- lm(wage ~ female + northcen + west + south, data = wages)
restricted_reg <- lm(wage ~ female, data = wages)

F-test Example II

  • Unrestricted model:

^Wagei=^β0+^β1Femalei+^β2Northeasti+^β3Northcen+^β4Southi

  • Restricted model:

^Wagei=^β0+^β1Femalei

  • H0:β2=β3=β4=0

  • q=3 restrictions (F numerator df)

  • n−k−1=526−4−1=521 (F denominator df)

F-test Example III

  • We can use the car package's linearHypothesis() command to run an F-test:
    • first argument: name of the (unrestricted) regression
    • second argument: vector of variable names (in quotes) you are testing

F-test Example III

  • We can use the car package's linearHypothesis() command to run an F-test:
    • first argument: name of the (unrestricted) regression
    • second argument: vector of variable names (in quotes) you are testing
# load car package for additional regression tools
library(car) 
# F-test
linearHypothesis(unrestricted_reg, c("northcen", "west", "south"))
## Linear hypothesis test
## 
## Hypothesis:
## northcen = 0
## west = 0
## south = 0
## 
## Model 1: restricted model
## Model 2: wage ~ female + northcen + west + south
## 
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
## 1    524 6332.2                                
## 2    521 6174.8  3    157.36 4.4258 0.004377 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F-test Example III

  • We can use the car package's linearHypothesis() command to run an F-test:
    • first argument: name of the (unrestricted) regression
    • second argument: vector of variable names (in quotes) you are testing
# load car package for additional regression tools
library(car) 
# F-test
linearHypothesis(unrestricted_reg, c("northcen", "west", "south"))
## Linear hypothesis test
## 
## Hypothesis:
## northcen = 0
## west = 0
## south = 0
## 
## Model 1: restricted model
## Model 2: wage ~ female + northcen + west + south
## 
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
## 1    524 6332.2                                
## 2    521 6174.8  3    157.36 4.4258 0.004377 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • p-value on F-test <0.05, so we can reject H0

Second F-test Example: Are Two Coefficients Equal?

  • The second type of test is whether two coefficients equal one another

Example:

^wagei=β0+β1Adolescent heighti+β2Adult heighti+β3Malei

Second F-test Example: Are Two Coefficients Equal?

  • The second type of test is whether two coefficients equal one another

Example:

^wagei=β0+β1Adolescent heighti+β2Adult heighti+β3Malei

  • Does height as an adolescent have the same effect on wages as height as an adult?

H0:β1=β2

Second F-test Example: Are Two Coefficients Equal?

  • The second type of test is whether two coefficients equal one another

Example:

^wagei=β0+β1Adolescent heighti+β2Adult heighti+β3Malei

  • Does height as an adolescent have the same effect on wages as height as an adult?

H0:β1=β2

  • What is the restricted regression?

^wagei=β0+β1(Adolescent heighti+Adult heighti)+β3Malei

  • q=1 restriction

Second F-test Example: Data

# load in data
heightwages <- read_csv("../data/heightwages.csv")
# make a "heights" variable as the sum of adolescent (height81) and adult (height85) height
heightwages <- heightwages %>%
  mutate(heights = height81 + height85)
height_reg <- lm(wage96 ~ height81 + height85 + male, data = heightwages)
height_restricted_reg <- lm(wage96 ~ heights + male, data = heightwages)

Second F-test Example: Data

  • For second argument, set two variables equal, in quotes
linearHypothesis(height_reg, "height81 = height85") # F-test
## Linear hypothesis test
## 
## Hypothesis:
## height81 - height85 = 0
## 
## Model 1: restricted model
## Model 2: wage96 ~ height81 + height85 + male
## 
##   Res.Df     RSS Df Sum of Sq      F Pr(>F)
## 1   6591 5128243                           
## 2   6590 5127284  1     959.2 1.2328 0.2669

  • Insufficient evidence to reject H0!

  • The effect of adolescent and adult height on wages is the same

All F-test I

summary(unrestricted_reg)
## 
## Call:
## lm(formula = wage ~ female + northcen + west + south, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.3269 -2.0105 -0.7871  1.1898 17.4146 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.5654     0.3466  21.827   <2e-16 ***
## female       -2.5652     0.3011  -8.520   <2e-16 ***
## northcen     -0.5918     0.4362  -1.357   0.1755    
## west          0.4315     0.4838   0.892   0.3729    
## south        -1.0262     0.4048  -2.535   0.0115 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.443 on 521 degrees of freedom
## Multiple R-squared:  0.1376,    Adjusted R-squared:  0.131 
## F-statistic: 20.79 on 4 and 521 DF,  p-value: 6.501e-16
  • Last line of regression output from summary() is an All F-test
    • H0: all β′s=0
      • the regression explains no variation in Y
    • Calculates an F-statistic that, if high enough, is significant (p-value <0.05) enough to reject H0

All F-test II

  • Alternatively, if you use broom instead of summary():
    • glance() command makes table of regression summary statistics
    • tidy() only shows coefficients
library(broom)
glance(unrestricted_reg)
## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
##       <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.138         0.131  3.44      20.8 6.50e-16     4 -1394. 2800. 2826.
## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
  • statistic is the All F-test, p.value next to it is the p-value from the F test

Outline

Natural Logarithms

Linear-Log Model

Log-Linear Model

Log-Log Model

Comparing Across Units

Joint Hypothesis Testing

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow