+ - 0:00:00
Notes for current slide
Notes for next slide

3.6 — Regression with Categorical Data

ECON 480 • Econometrics • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/metricsF21
metricsF21.classes.ryansafner.com

Outline

Working with Factor Variables in R

Regression with Dummy Variables

Recoding Dummies

Categorical Variables (More than 2 Categories)

Categorical Data

  • Categorical data place an individual into one of several possible categories

    • e.g. sex, season, political party
    • may be responses to survey questions
    • can be quantitative (e.g. age, zip code)

  • R calls these factors

Working with factor Variables in R

Factors in R

  • factor is a special type of character object class that indicates membership in a category (called a level)

  • Suppose I have data on students:

students %>% head(n = 5)
ABCDEFGHIJ0123456789
ID
<dbl>
Rank
<chr>
Grade
<dbl>
1Sophomore77
2Senior72
3Freshman73
4Senior73
5Junior84
5 rows

Factors in R

  • factor is a special type of character object class that indicates membership in a category (called a level)

  • Suppose I have data on students:

students %>% head(n = 5)
ABCDEFGHIJ0123456789
ID
<dbl>
Rank
<chr>
Grade
<dbl>
1Sophomore77
2Senior72
3Freshman73
4Senior73
5Junior84
5 rows
  • See that Rank is a character (<chr>) variable, just a string of text

Factors in R

  • We can make Rank a factor variable, to indicate a student is a member of one of the possible categories: (freshman, sophomore, junior, senior)
students <- students %>%
  mutate(Rank = as.factor(Rank)) # overwrite and change class of Rank to factor
students %>% head(n = 5)
ABCDEFGHIJ0123456789
ID
<dbl>
Rank
<fct>
Grade
<dbl>
1Sophomore77
2Senior72
3Freshman73
4Senior73
5Junior84
5 rows
  • See now it’s a factor (<fct>)

Factors in R

# what are the categories?
students %>%
  group_by(Rank) %>%
  count()
ABCDEFGHIJ0123456789
Rank
<fct>
n
<int>
Freshman1
Junior4
Senior2
Sophomore3
4 rows
# note the order is arbitrary! This is an "unordered" factor

Ordered Factors in R

  • If there is a rank order you wish to preserve, you can make an ordered (factor) variable
    • list the levels from 1st to last
students <- students %>%
  mutate(Rank = ordered(Rank, # overwrite and change class of Rank to ordered
                        # next, specify the levels, in order
                        levels = c("Freshman", "Sophomore", "Junior", "Senior")
                        )
         )
students %>% head(n = 5)
ABCDEFGHIJ0123456789
ID
<dbl>
Rank
<ord>
Grade
<dbl>
1Sophomore77
2Senior72
3Freshman73
4Senior73
5Junior84
5 rows

Ordered Factors in R

students %>%
  group_by(Rank) %>%
  count()
ABCDEFGHIJ0123456789
Rank
<ord>
n
<int>
Freshman1
Sophomore3
Junior4
Senior2
4 rows

Example Research Question

Example: How much higher wages, on average, do men earn compared to women?

The Pure Statistics of Comparing Group Means

  • Basic statistics: can test for statistically significant difference in group means with a t-test†, let:

  • YM: average earnings of a sample of nM men

  • YW: average earnings of a sample of nW women

  • Difference in group averages: d= ˉYM − ˉYW

  • The hypothesis test is:

    • H0:d=0
    • H1:d≠0

† See today’s class page for this example

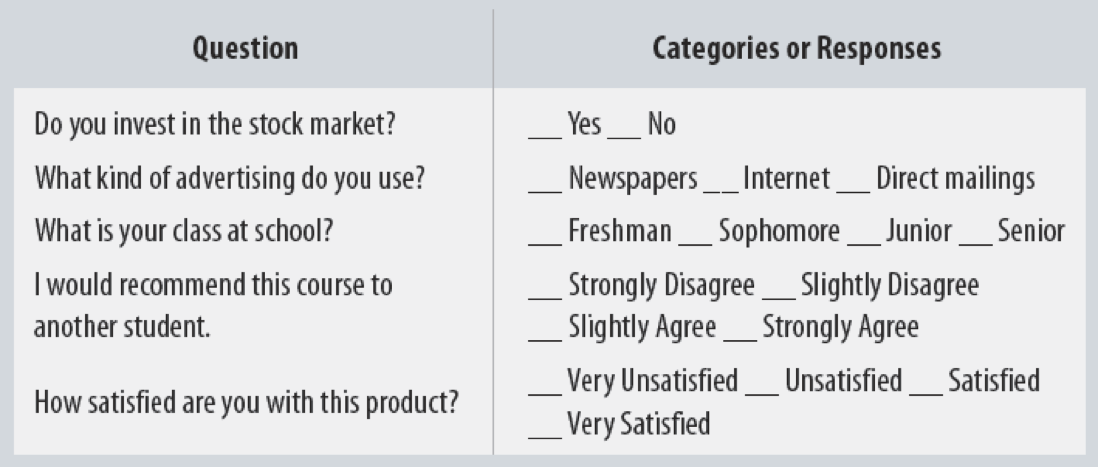
Plotting Factors in R

  • If I plot a factor variable, e.g. Gender (which is either Male or Female), the scatterplot with wage looks like this

    • effectively R treats values of a factor variable as integers
    • in this case, "Female" = 0, "Male" = 1

  • Let’s make this more explicit by making a dummy variable to stand in for Gender

Regression with Dummy Variables

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable†

  • Dummy variable only =0 or =1, if a condition is TRUE vs. FALSE

  • Signifies whether an observation belongs to a category or not

† Also called a binary variable or dichotomous variable

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable†

  • Dummy variable only =0 or =1, if a condition is TRUE vs. FALSE

  • Signifies whether an observation belongs to a category or not

† Also called a binary variable or dichotomous variable

Example:

^Wagei=^β0+^β1Femalei where Femalei={1if individual i is Female0if individual i is Male

Comparing Groups with Regression

  • In a regression, we can easily compare across groups via a dummy variable†

  • Dummy variable only =0 or =1, if a condition is TRUE vs. FALSE

  • Signifies whether an observation belongs to a category or not

† Also called a binary variable or dichotomous variable

Example:

^Wagei=^β0+^β1Femalei where Femalei={1if individual i is Female0if individual i is Male

  • Again, ^β1 makes less sense as the “slope” of a line in this context

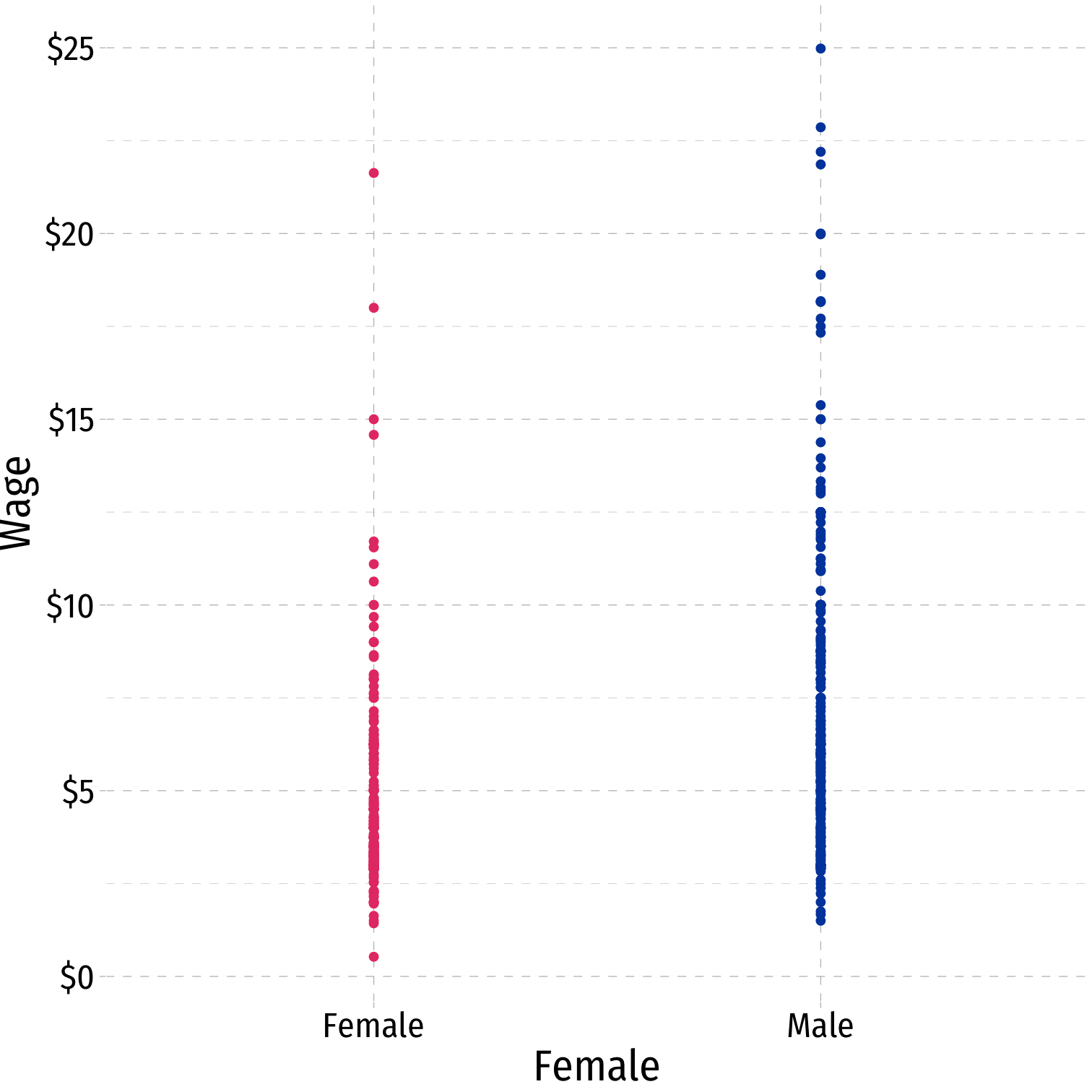
Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

  • Tip: use geom_jitter() instead of geom_point() to randomly nudge points to see them better!

    • Only used for plotting, does not affect actual data, regression, etc.

Comparing Groups in Regression: Scatterplot

  • Female is our dummy x-variable

  • Hard to see relationships because of overplotting

  • Use geom_jitter() instead of geom_point() to randomly nudge points

    • Only for plotting purposes, does not affect actual data, regression, etc.

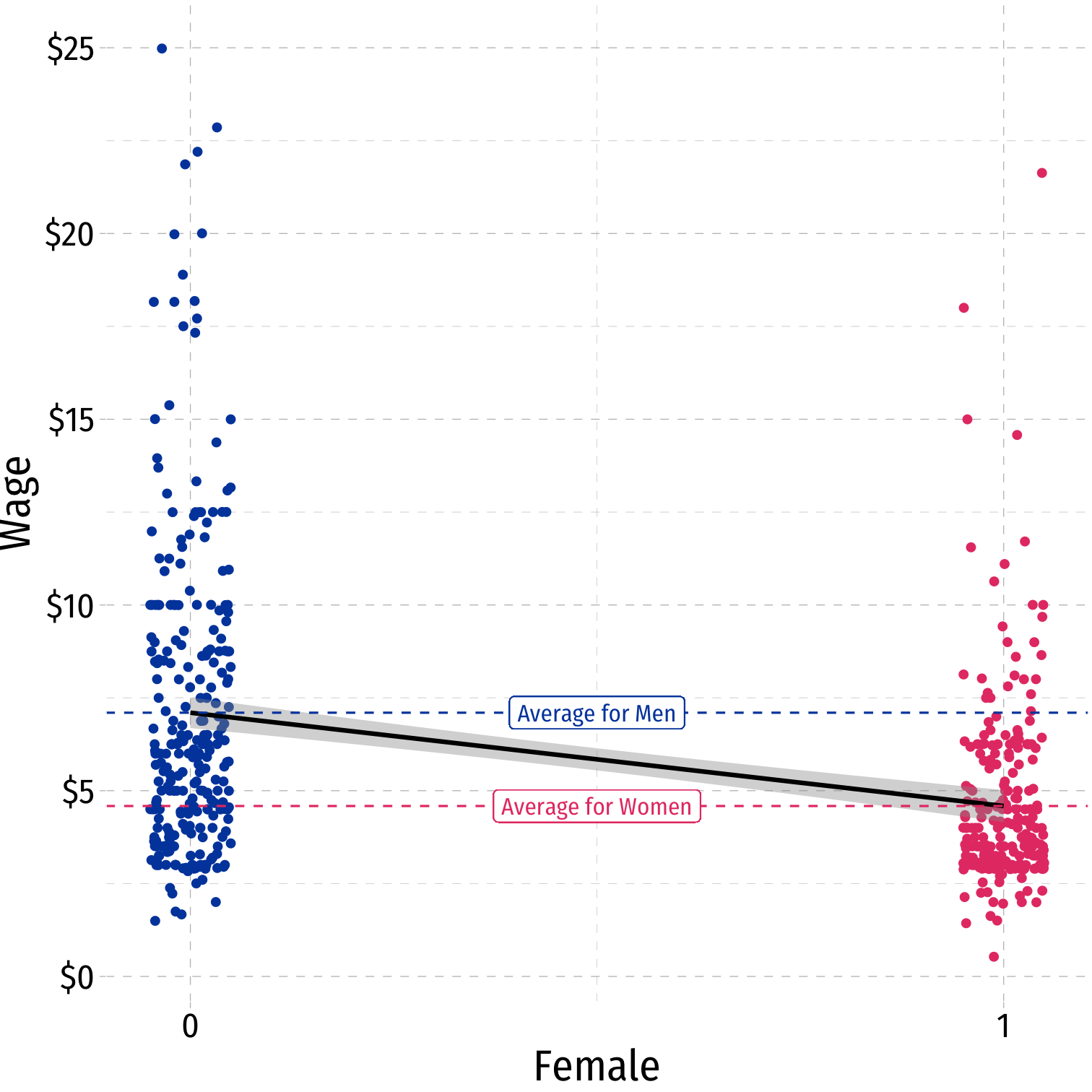
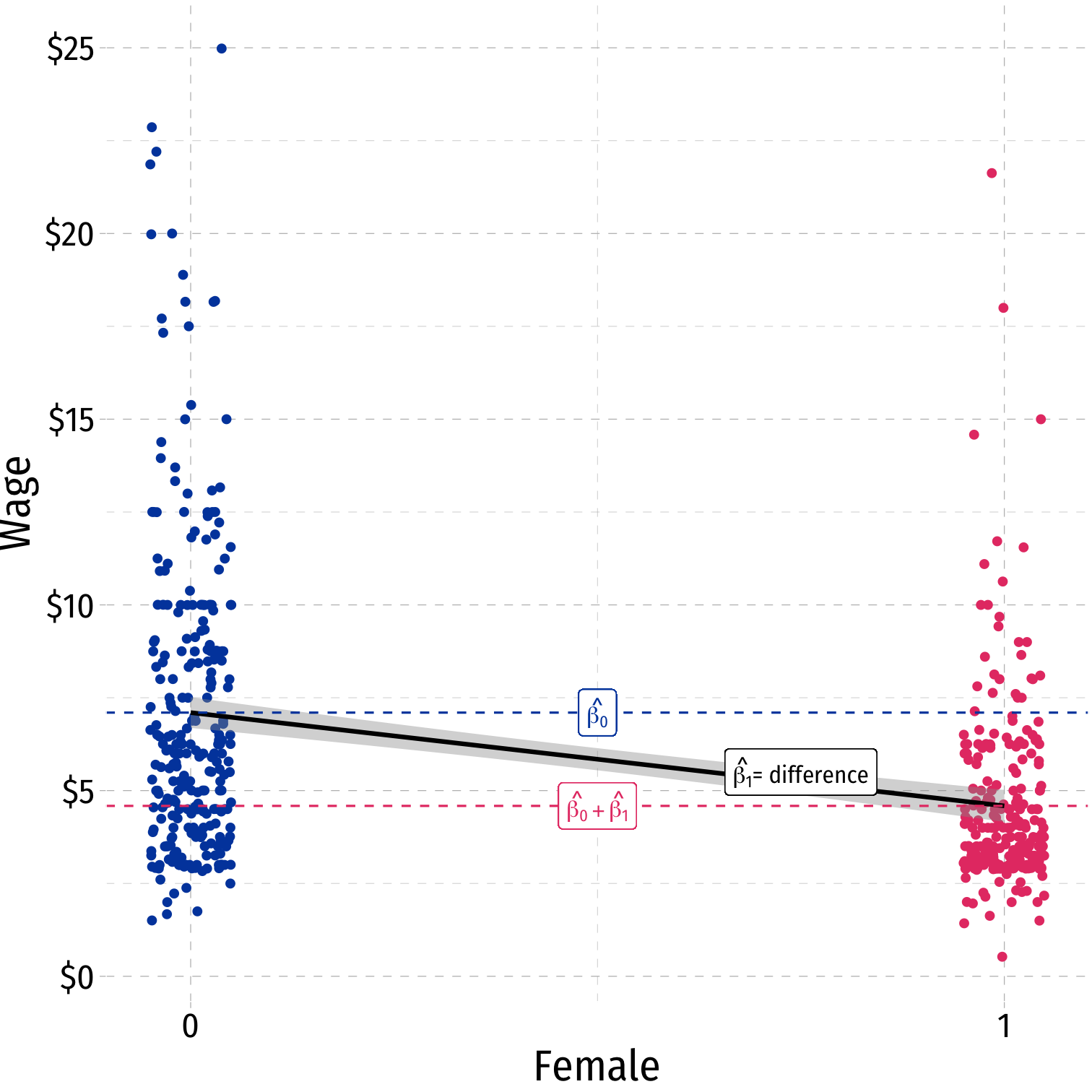
Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (“Control group”):
    • ^Yi=^β0
    • E[Yi|Di=0]=^β0 ⟺ the mean of Y when Di=0

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (“Control group”):
    • ^Yi=^β0
    • E[Yi|Di=0]=^β0 ⟺ the mean of Y when Di=0
  • When Di=1 (“Treatment group”):
    • ^Yi=^β0+^β1Di
    • E[Yi|Di=1]=^β0+^β1 ⟺ the mean of Y when Di=1

Dummy Variables as Group Means

^Yi=^β0+^β1Di where Di={0,1}

  • When Di=0 (“Control group”):
    • ^Yi=^β0
    • E[Yi|Di=0]=^β0 ⟺ the mean of Y when Di=0
  • When Di=1 (“Treatment group”):
    • ^Yi=^β0+^β1Di
    • E[Yi|Di=1]=^β0+^β1 ⟺ the mean of Y when Di=1
  • So the difference in group means:

=E[Yi|Di=1]−E[Yi|Di=0]=(^β0+^β1)−(^β0)=^β1

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

  • Difference in wage between men & women:

Dummy Variables as Group Means: Our Example

Example:

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

  • Mean wage for men: E[Wage|Female=0]=^β0

  • Mean wage for women: E[Wage|Female=1]=^β0+^β1

  • Difference in wage between men & women: ^β1

Comparing Groups in Regression: Scatterplot

^Wagei=^β0+^β1Femalei

where Femalei={1if i is Female0if i is Male

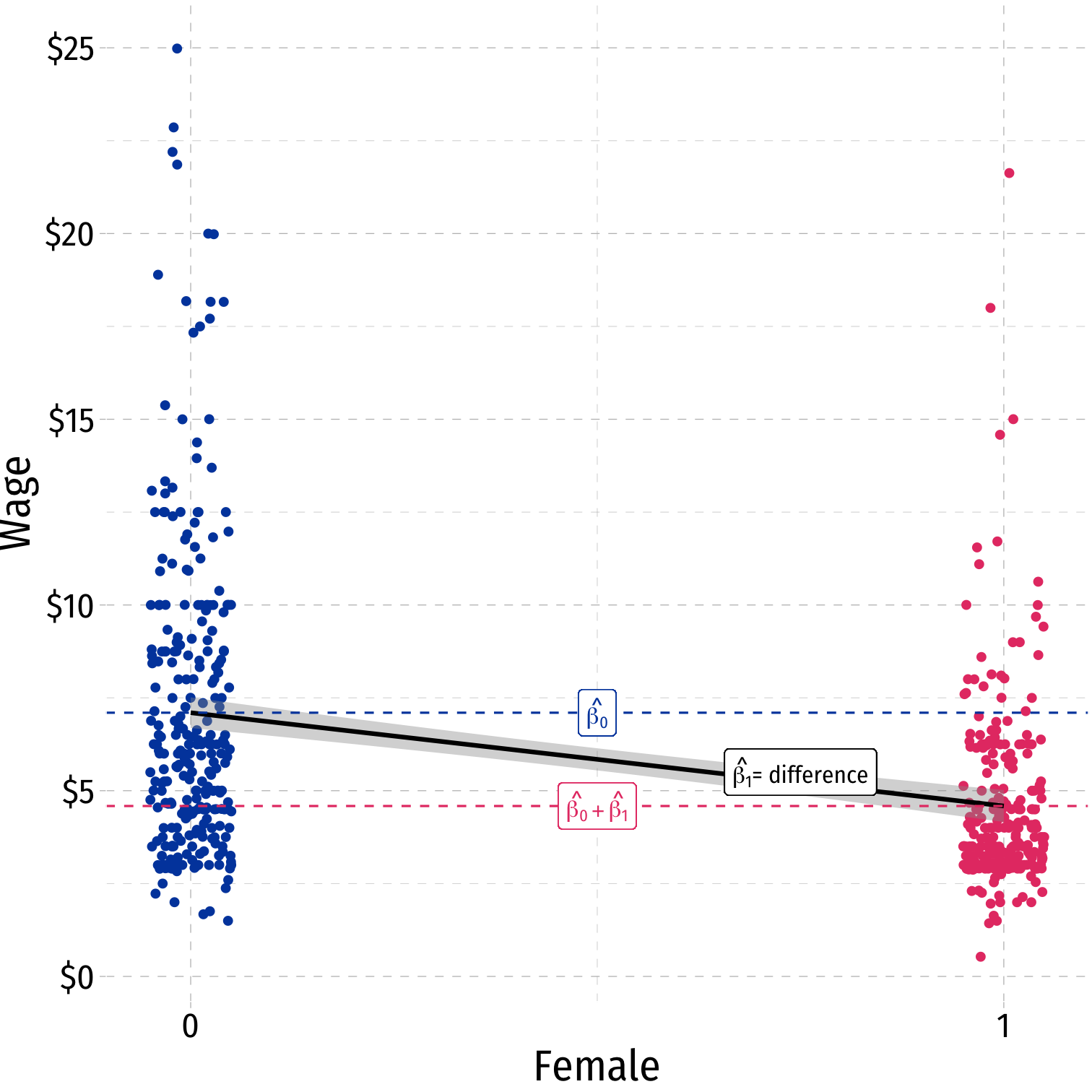
The Data

# comes from wooldridge package
# install.packages("wooldridge")
library(wooldridge)
# data is called "wage1", save as a dataframe I'll call "wages"
wages <- wage1
wages %>% head()

Get Group Averages & Std. Devs.

# Summarize for Men
wages %>%
  filter(female==0) %>%
  summarize(mean = mean(wage),
            sd = sd(wage))
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
7.0994894.160858
1 row
# Summarize for Women
wages %>%
  filter(female==1) %>%
  summarize(mean = mean(wage),
            sd = sd(wage))
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
4.5876592.529363
1 row

Visualize Differences

The Regression I

femalereg <- lm(wage ~ female, data = wages)
summary(femalereg)
## 
## Call:
## lm(formula = wage ~ female, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.0995     0.2100  33.806  < 2e-16 ***
## female       -2.5118     0.3034  -8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15

The Regression I

femalereg <- lm(wage ~ female, data = wages)
summary(femalereg)
## 
## Call:
## lm(formula = wage ~ female, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.0995     0.2100  33.806  < 2e-16 ***
## female       -2.5118     0.3034  -8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15
library(broom)
tidy(femalereg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)7.0994890.210008233.805777
female-2.5118300.3034092-8.278688
2 rows | 1-4 of 5 columns

Dummy Regression vs. Group Means

From tabulation of group means

Gender Avg. Wage Std. Dev. n
Female 4.59 2.33 252
Male 7.10 4.16 274
Difference 2.51 0.30 −

From t-test of difference in group means

ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
(Intercept)7.0994890.2100082
female-2.5118300.3034092
2 rows | 1-3 of 5 columns

^Wagesi=7.10−2.51Femalei

Recoding Dummies

Recoding Dummies

Example:

  • Suppose instead of female we had used:

^Wagei=^β0+^β1Malei where Malei={1if person i is Male0if person i is Female

Recoding Dummies with Data

wages<-wages %>%
  mutate(male = ifelse(female == 0, # condition: is female equal to 0?
                       yes = 1, # if true: code as "1"
                       no = 0)) # if false: code as "0"
# verify it worked
wages %>% 
  select(wage, female, male) %>%
  head()
ABCDEFGHIJ0123456789
 
 
wage
<dbl>
female
<int>
male
<dbl>
13.1010
23.2410
33.0001
46.0001
55.3001
68.7501
6 rows

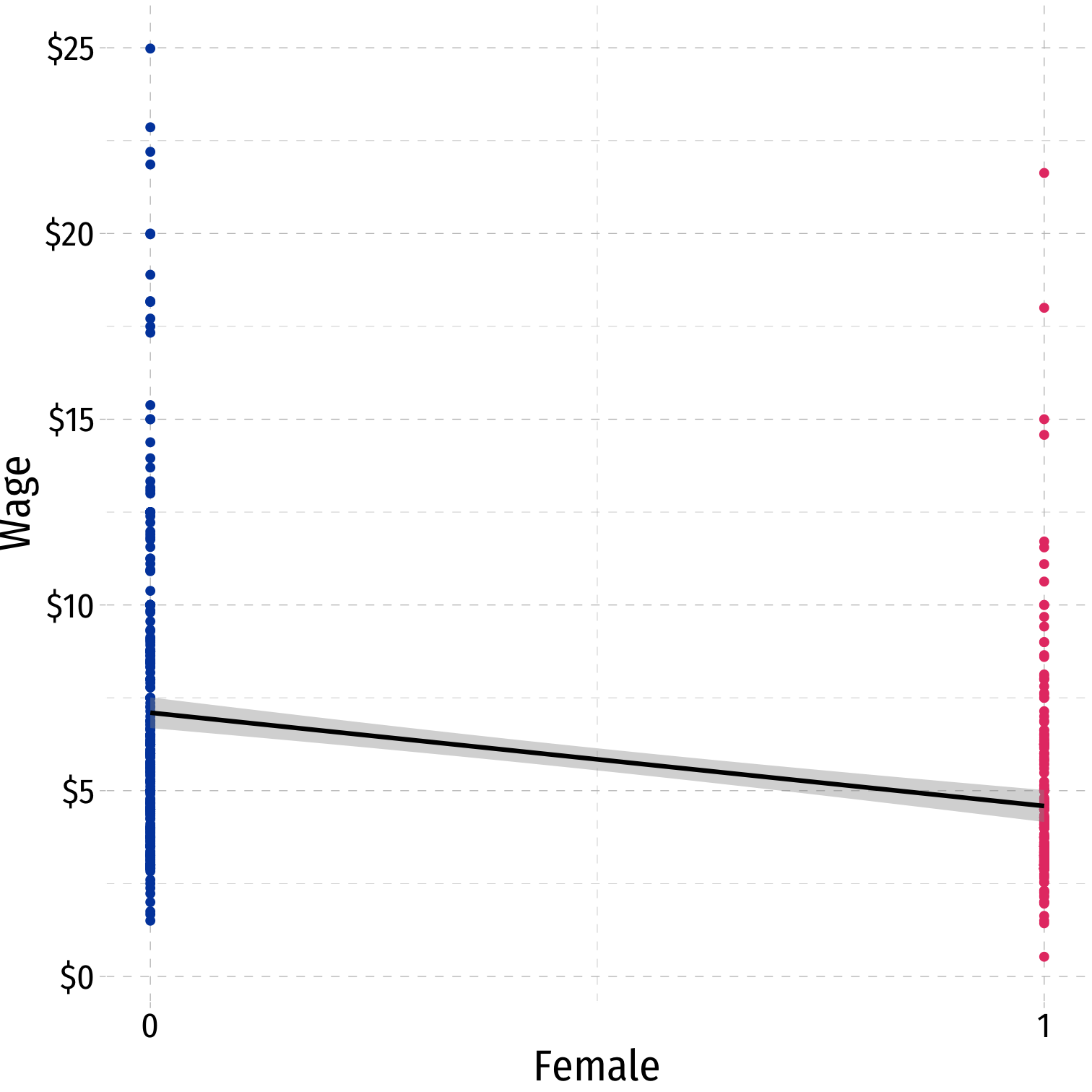
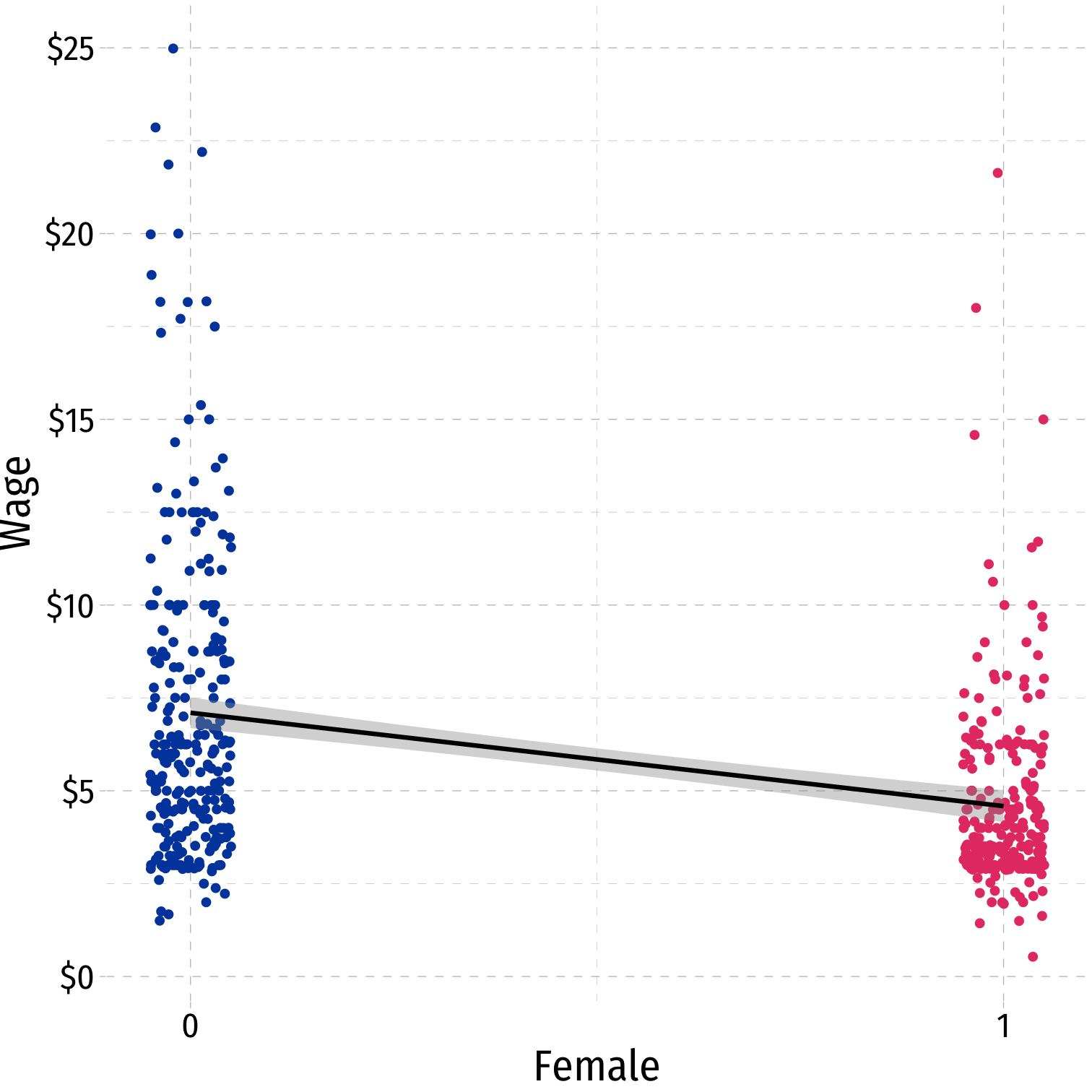
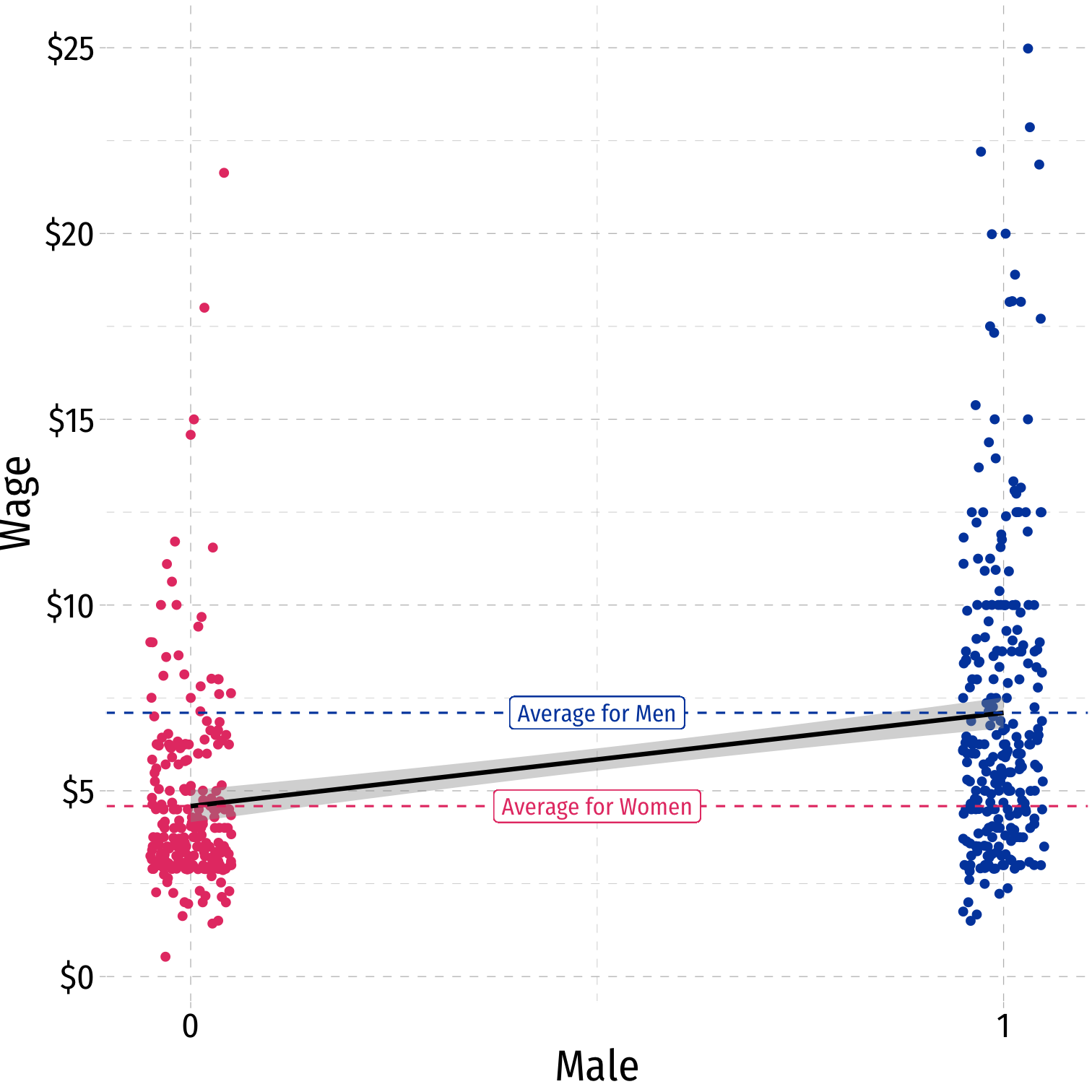
Scatterplot with Male

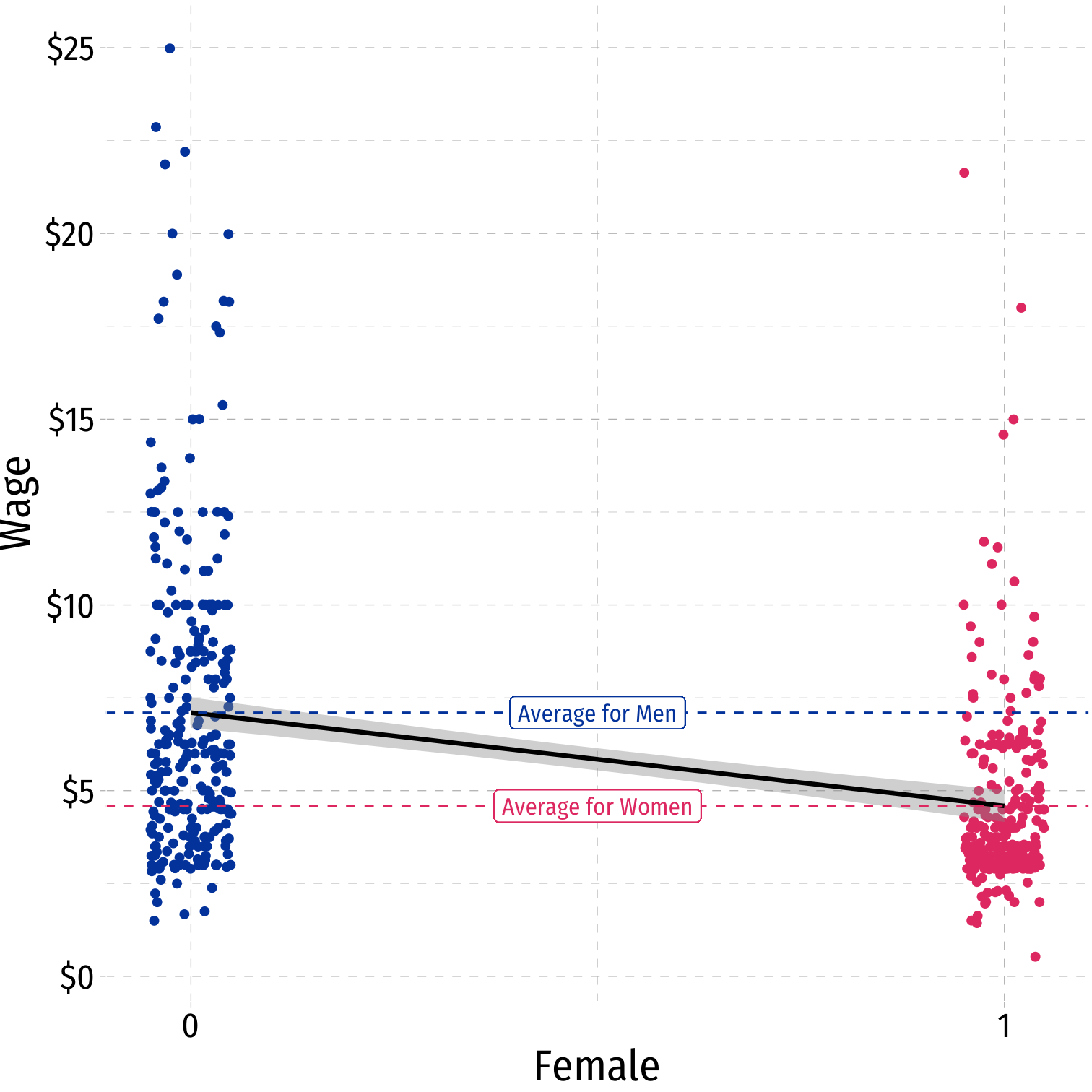
Scatterplot with Male

Dummy Variables as Group Means: With Male

Example:

^Wagei=^β0+^β1Malei

where Malei={1if i is Male0if i is Female

  • Mean wage for men: E[Wage|Male=1]=^β0+^β1

  • Mean wage for women: E[Wage|Male=0]=^β0

  • Difference in wage between men & women: ^β1

Scatterplot with Male

Scatterplot with Male

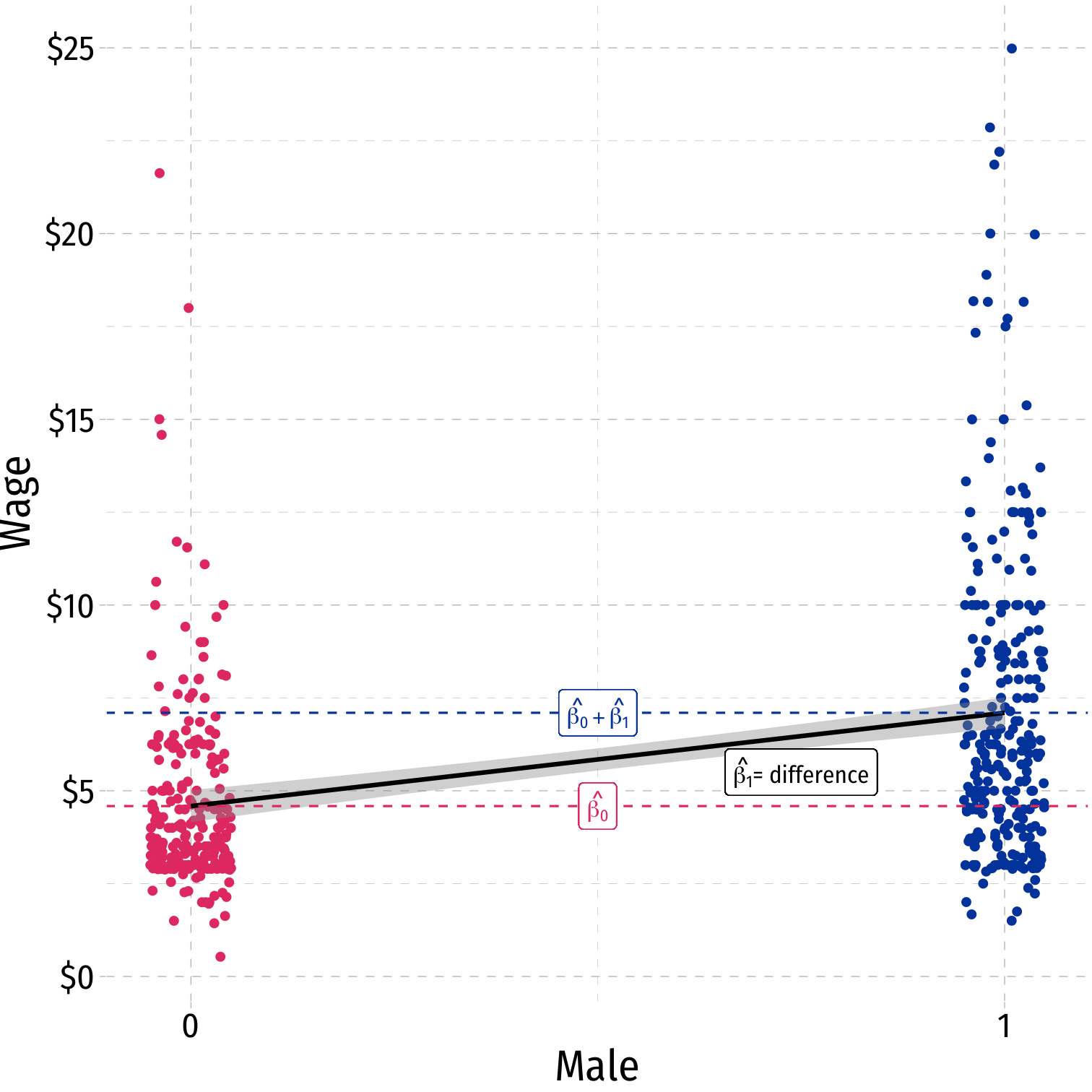
The Regression with Male I

malereg <- lm(wage ~ male, data = wages)
summary(malereg)
## 
## Call:
## lm(formula = wage ~ male, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.5877     0.2190  20.950  < 2e-16 ***
## male          2.5118     0.3034   8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15

The Regression with Male I

malereg <- lm(wage ~ male, data = wages)
summary(malereg)
## 
## Call:
## lm(formula = wage ~ male, data = wages)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.5877     0.2190  20.950  < 2e-16 ***
## male          2.5118     0.3034   8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157,    Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15
library(broom)
tidy(malereg)
ABCDEFGHIJ0123456789
term
<chr>
estimate
<dbl>
std.error
<dbl>
statistic
<dbl>
(Intercept)4.5876590.218983420.949802
male2.5118300.30340928.278688
2 rows | 1-4 of 5 columns

The Dummy Regression: Male or Female

(1)(2)
Constant4.59 ***7.10 ***
(0.22)   (0.21)   
Female       -2.51 ***
       (0.30)   
Male2.51 ***       
(0.30)          
N526       526       
R-Squared0.12    0.12    
SER3.48    3.48    
*** p < 0.001; ** p < 0.01; * p < 0.05.

  • Note it doesn't matter if we use male or female, males always earn $2.51 more than females

  • Compare the constant (average for the D=0 group)

  • Should you use male AND female? We'll come to that...

Categorical Variables (More than 2 Categories)

Categorical Variables with More than 2 Categories

  • A categorical variable expresses membership in a category, where there is no ranking or hierarchy of the categories
    • We've looked at categorical variables with 2 categories only
    • e.g. Male/Female, Spring/Summer/Fall/Winter, Democratic/Republican/Independent

Categorical Variables with More than 2 Categories

  • A categorical variable expresses membership in a category, where there is no ranking or hierarchy of the categories
    • We've looked at categorical variables with 2 categories only
    • e.g. Male/Female, Spring/Summer/Fall/Winter, Democratic/Republican/Independent
  • Might be an ordinal variable expresses rank or an ordering of data, but not necessarily their relative magnitude
    • e.g. Order of finalists in a competition (1st, 2nd, 3rd)
    • e.g. Highest education attained (1=elementary school, 2=high school, 3=bachelor's degree, 4=graduate degree)

Using Categorical Variables in Regression I

Example: How do wages vary by region of the country? Let Regioni={Northeast,Midwest,South,West}

Using Categorical Variables in Regression I

Example: How do wages vary by region of the country? Let Regioni={Northeast,Midwest,South,West}

  • Can we run the following regression?

^Wagesi=^β0+^β1Regioni

Using Categorical Variables in Regression II

Example: How do wages vary by region of the country?

Code region numerically: Regioni={1if i is in Northeast2if i is in Midwest3if i is in South4if i is in West

Using Categorical Variables in Regression II

Example: How do wages vary by region of the country?

Code region numerically: Regioni={1if i is in Northeast2if i is in Midwest3if i is in South4if i is in West

  • Can we run the following regression?

^Wagesi=^β0+^β1Regioni

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0
  • Can we run the following regression?

^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

Using Categorical Variables in Regression III

Example: How do wages vary by region of the country?

Create a dummy variable for each region:

  • Northeasti=1 if i is in Northeast, otherwise =0
  • Midwesti=1 if i is in Midwest, otherwise =0
  • Southi=1 if i is in South, otherwise =0
  • Westi=1 if i is in West, otherwise =0
  • Can we run the following regression?

^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

  • For every i:Northeasti+Midwesti+Southi+Westi=1!

The Dummy Variable Trap

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi+^β4Westi

  • If we include all possible categories, they are perfectly multicollinear, an exact linear function of one another:

Northeasti+Midwesti+Southi+Westi=1∀i

  • This is known as the dummy variable trap, a common source of perfect multicollinearity

The Reference Category

  • To avoid the dummy variable trap, always omit one category from the regression, known as the “reference category”

  • It does not matter which category we omit!

  • Coefficients on each dummy variable measure the difference between the reference category and each category dummy

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

  • ^β3:

The Reference Category: Example

Example: ^Wagesi=^β0+^β1Northeasti+^β2Midwesti+^β3Southi

  • Westi is omitted (arbitrarily chosen)

  • ^β0: average wage for i in the West

  • ^β1: difference between West and Northeast

  • ^β2: difference between West and Midwest

  • ^β3: difference between West and South

Dummy Variable Trap in R

lm(wage ~ noreast + northcen + south + west, data = wages) %>% summary()
## 
## Call:
## lm(formula = wage ~ noreast + northcen + south + west, data = wages)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -6.083 -2.387 -1.097  1.157 18.610 
## 
## Coefficients: (1 not defined because of singularities)
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   6.6134     0.3891  16.995  < 2e-16 ***
## noreast      -0.2436     0.5154  -0.473  0.63664    
## northcen     -0.9029     0.5035  -1.793  0.07352 .  
## south        -1.2265     0.4728  -2.594  0.00974 ** 
## west              NA         NA      NA       NA    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.671 on 522 degrees of freedom
## Multiple R-squared:  0.0175,    Adjusted R-squared:  0.01185 
## F-statistic: 3.099 on 3 and 522 DF,  p-value: 0.02646

Using Different Reference Categories in R

# let's run 4 regressions, each one we omit a different region
no_noreast_reg <- lm(wage ~ northcen + south + west, data = wages)
no_northcen_reg <- lm(wage ~ noreast + south + west, data = wages)
no_south_reg <- lm(wage ~ noreast + northcen + west, data = wages)
no_west_reg <- lm(wage ~ noreast + northcen + south, data = wages)
# now make an output table
library(huxtable)
huxreg(no_noreast_reg,
       no_northcen_reg,
       no_south_reg,
       no_west_reg,
       coefs = c("Constant" = "(Intercept)",
                 "Northeast" = "noreast",
                 "Midwest" = "northcen",
                 "South" = "south",
                 "West" = "west"),
       statistics = c("N" = "nobs",
                      "R-Squared" = "r.squared",
                      "SER" = "sigma"),
       number_format = 3)

Using Different Reference Categories in R II

(1)(2)(3)(4)
Constant6.370 ***5.710 ***5.387 ***6.613 ***
(0.338)   (0.320)   (0.268)   (0.389)   
Northeast        0.659    0.983 *  -0.244    
        (0.465)   (0.432)   (0.515)   
Midwest-0.659            0.324    -0.903    
(0.465)           (0.417)   (0.504)   
South-0.983 *  -0.324            -1.226 ** 
(0.432)   (0.417)           (0.473)   
West0.244    0.903    1.226 **         
(0.515)   (0.504)   (0.473)           
N526        526        526        526        
R-Squared0.017    0.017    0.017    0.017    
SER3.671    3.671    3.671    3.671    
*** p < 0.001; ** p < 0.01; * p < 0.05.

  • Constant is alsways average wage for reference (omitted) region

  • Compare coefficients between Midwest in (1) and Northeast in (2)...

  • Compare coefficients between West in (3) and South in (4)...

  • Does not matter which region we omit!

    • Same R2, SER, coefficients give same results

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent (Y) variable be a dummy variable

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent (Y) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent (Y) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

  • A model where Y is a dummy is called a linear probability model, as it measures the probability of Y occuring (=1) given the X's, i.e. P(Yi=1|X1,⋯,Xk)
    • e.g. the probability person i is Admitted to a program with a given GPA

Dummy Dependent (Y) Variables

  • In many contexts, we will want to have our dependent (Y) variable be a dummy variable

Example: ^Admittedi=^β0+^β1GPAi where Admittedi={1if i is Admitted0if i is Not Admitted

  • A model where Y is a dummy is called a linear probability model, as it measures the probability of Y occuring (=1) given the X's, i.e. P(Yi=1|X1,⋯,Xk)
    • e.g. the probability person i is Admitted to a program with a given GPA

  • Requires special tools to properly interpret and extend this (logit, probit, etc)

  • Feel free to write papers that have dummy Y variables (but you may have to ask me some more questions)!

Outline

Working with Factor Variables in R

Regression with Dummy Variables

Recoding Dummies

Categorical Variables (More than 2 Categories)

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow