Overview
Today, we finish up our view of nonlinear models with logarithmic models, which are more frequently used. We also discuss a few other tests and transformations to wrap up multivariate regression before we turn to panel data: standardizing variables to compare effect sizes, and joint hypothesis tests.
Interpretting logged variables can often be difficult to remember, so here I reproduce the tables that describe the interpretations of the marginal effect of \(X \rightarrow Y\), as well as some visual examples from the slides:
| Model | Equation | Interpretation |
|---|---|---|
| Linear-Log | \(Y=\beta_0+\beta_1 \mathbf{ln(X)}\) | 1% change in \(X \rightarrow \frac{\hat{\beta_1}}{100}\) unit change in \(Y\) |
| Log-Linear | \(\mathbf{ln(Y)}=\beta_0+\beta_1X\) | 1 unit change in \(X \rightarrow \hat{\beta_1}\times 100\)% change in \(Y\) |
| Log-Log | \(\mathbf{ln(Y)}=\beta_0+\beta_1\mathbf{ln(X)}\) | 1% change in \(X \rightarrow \hat{\beta_1}\)% change in \(Y\) |
- Hint: the variable that gets logged changes in percent terms, the variable not logged changes in unit terms
| Linear-Log | Log-Linear | Log-Log |
|---|---|---|
 |
 |
 |
| \(\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}\mathbf{ln(X_i)}\) | \(\mathbf{ln(\hat{Y_i})}=\hat{\beta_0}+\hat{\beta_1}X_i\) | \(\mathbf{ln(\hat{Y_i})}=\hat{\beta_0}+\hat{\beta_1}\mathbf{ln(X_i)}\) |
| \(R^2=0.65\) | \(R^2=0.30\) | \(R^2=0.61\) |
Readings
- Ch. 7.1 in Bailey, Real Econometrics
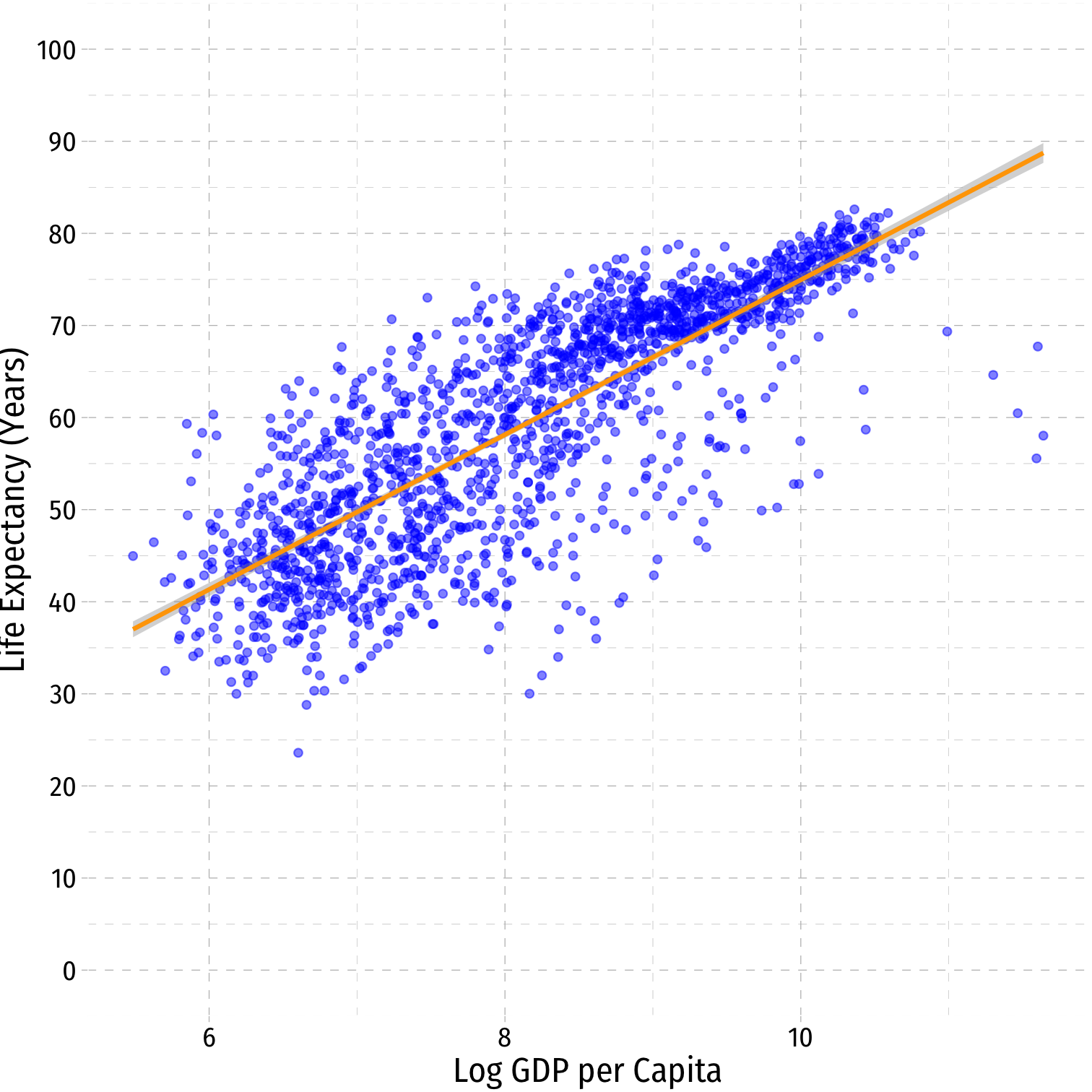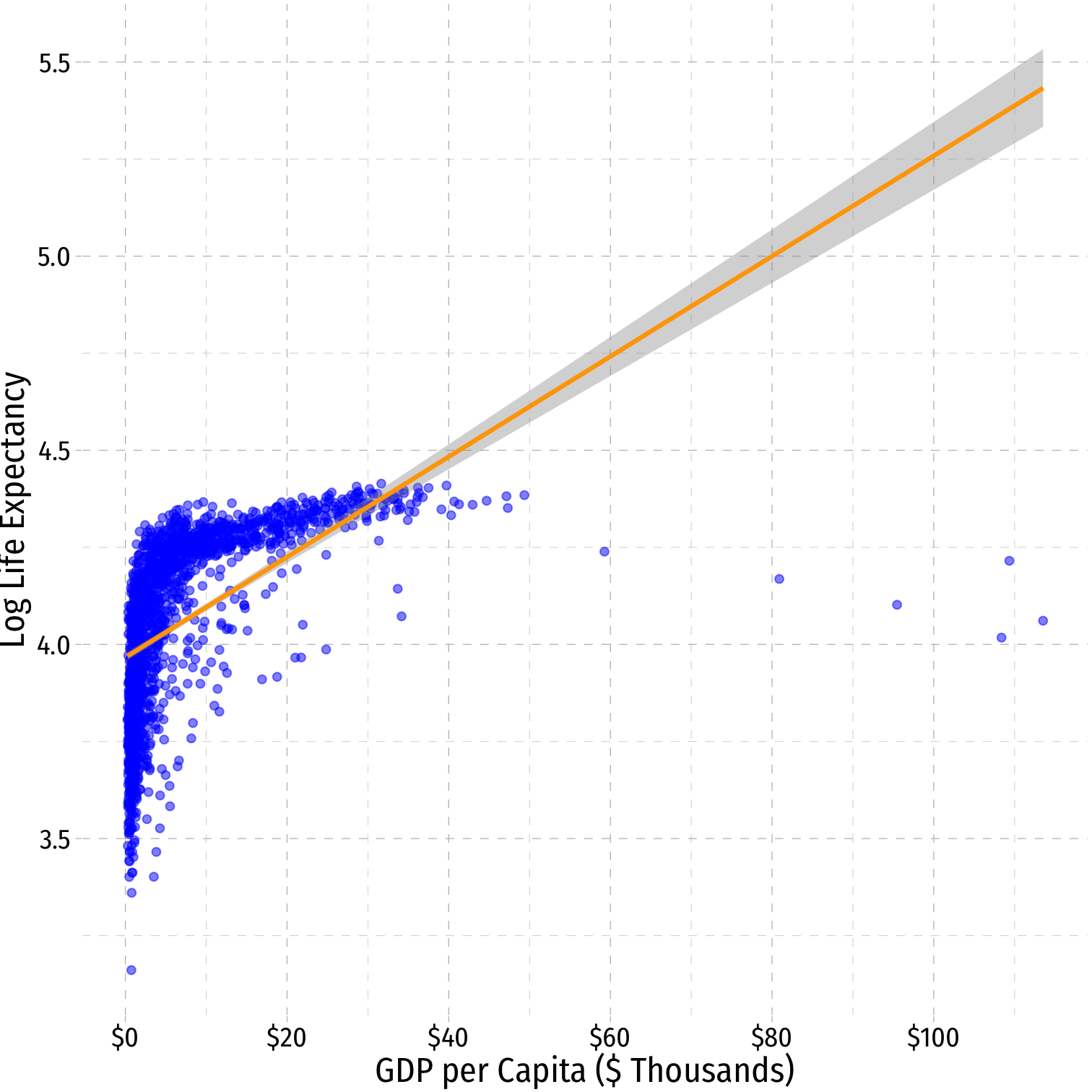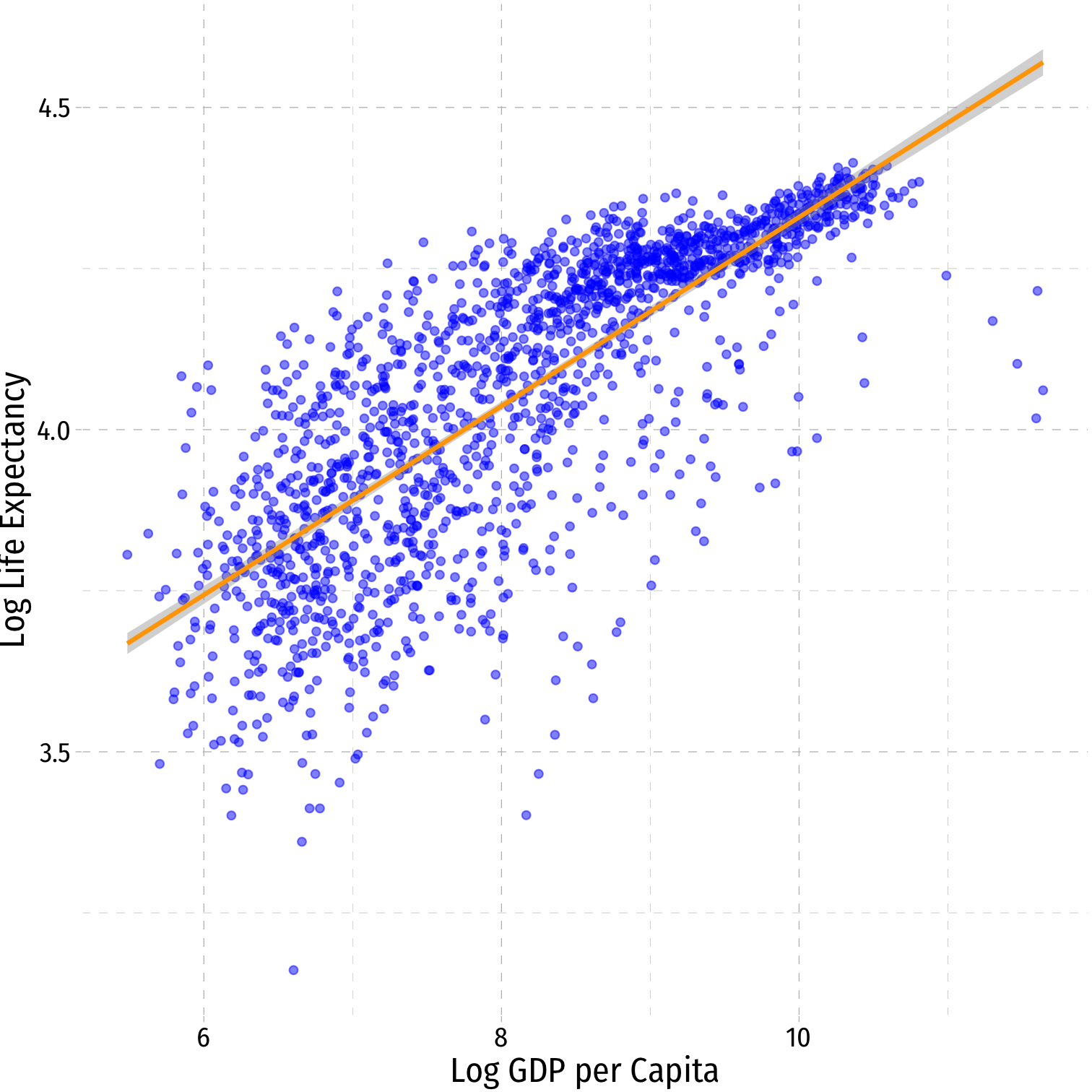Slides
Below, you can find the slides in two formats. Clicking the image will bring you to the html version of the slides in a new tab. Note while in going through the slides, you can type h to see a special list of viewing options, and type o for an outline view of all the slides.
The lower button will allow you to download a PDF version of the slides. I suggest printing the slides beforehand and using them to take additional notes in class (not everything is in the slides)!
Assignments
Problem Set 5 Due Tues Nov 23
Problem Set 5 is due by the end of the day on Tuesday, November 23. This will be your final graded homework!